题目内容
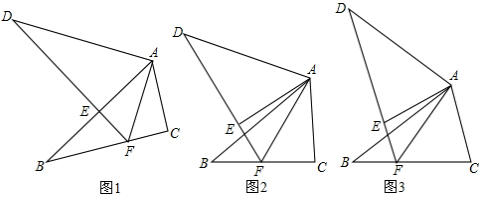
在平面直角坐标系中,抛物线y=ax2-
x+2过点B(1,0).
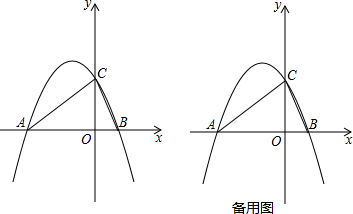
(1)求抛物线与y轴的交点C的坐标及与x轴的另一交点A的坐标;
(2)以AC为边在第二象限画正方形ACPQ,求P、Q两点的坐标;
(3)把(2)中的正方形ACPQ和抛物线沿射线AC一起运动,当运动到点Q与y轴重合时,求运动后的抛物线的顶点坐标.
| 4 |
| 3 |

(1)求抛物线与y轴的交点C的坐标及与x轴的另一交点A的坐标;
(2)以AC为边在第二象限画正方形ACPQ,求P、Q两点的坐标;
(3)把(2)中的正方形ACPQ和抛物线沿射线AC一起运动,当运动到点Q与y轴重合时,求运动后的抛物线的顶点坐标.
考点:二次函数综合题
专题:
分析:(1)根据解析式即可求得C点的坐标,应用待定系数法,求得a,然后令y=0,解方程即可求得A的坐标.
(2)依据三角形全等即可P、Q两点的坐标;
(3)设直线PQ的解析式为y=kx+b,利用待定系数法求得解析式,求得与y轴的交点Q′(0,
),点Q(-5,3)移动到点Q′(0,
),向右平移了5个单位长度,向上平移了
个单位长度,顶点(-1,
)移动后应是(4,6).
(2)依据三角形全等即可P、Q两点的坐标;
(3)设直线PQ的解析式为y=kx+b,利用待定系数法求得解析式,求得与y轴的交点Q′(0,
| 19 |
| 3 |
| 19 |
| 3 |
| 10 |
| 3 |
| 8 |
| 3 |
解答:解:(1)把B(1,0)代入抛物线y=ax2-
x+2,
得a-
+2=0,
解得a=-
.
所以y=-
x2-
x+2,
当x=0时,y=2,
所以抛物线与y轴交点C的坐标为(0,2).
当y=0时,-
x2-
x+2=0,
解得x1=1,x2=-3,
所以抛物线与x轴的另一个交点A的坐标为(-3,0);

(2)过P点作PE⊥y轴于E,过点Q作QF⊥x轴于F.
∵四边形ACPQ是正方形,
∴AC=CP=AQ,∠QAC=∠ACP=90°,
∴∠ACO+∠PCE=90°,
∵∠AOC=90°,
∴∠ACO+∠OAC=90°,
∴∠OAC=∠PCE,
在△AOC与△PCE中,
,
∴△AOC≌△PCE(AAS),
∴PE=OC=2,CE=AO=3,
∴OE=OC+CE=5,
∴点P的坐标为(-2,5).
同理△AOC≌△QFA,
∴QF=AO=3,AF=OC=2,
∴OF=AF+OA=5,
∴点Q的坐标为(-5,3);
(3)设直线PQ的解析式为y=kx+b
把P(-2,5),Q(-5,3)代入y=kx+b得
解,
得
.
∴y=
x+
,
∴当x=0时,y=
∴直线PQ与y轴的交点Q′(0,
),
∴点Q(-5,3)运动到点Q′(0,
).
∴向右平移了5个单位长度,向上平移了
个单位长度.
∵抛物线y=-
x2-
x+2的顶点为(-1,
)
∴运动后的抛物线的顶点坐标为(4,6).
| 4 |
| 3 |
得a-
| 4 |
| 3 |
解得a=-
| 2 |
| 3 |
所以y=-
| 2 |
| 3 |
| 4 |
| 3 |
当x=0时,y=2,
所以抛物线与y轴交点C的坐标为(0,2).
当y=0时,-
| 2 |
| 3 |
| 4 |
| 3 |
解得x1=1,x2=-3,
所以抛物线与x轴的另一个交点A的坐标为(-3,0);

(2)过P点作PE⊥y轴于E,过点Q作QF⊥x轴于F.
∵四边形ACPQ是正方形,
∴AC=CP=AQ,∠QAC=∠ACP=90°,
∴∠ACO+∠PCE=90°,
∵∠AOC=90°,
∴∠ACO+∠OAC=90°,
∴∠OAC=∠PCE,
在△AOC与△PCE中,
|
∴△AOC≌△PCE(AAS),
∴PE=OC=2,CE=AO=3,
∴OE=OC+CE=5,
∴点P的坐标为(-2,5).
同理△AOC≌△QFA,
∴QF=AO=3,AF=OC=2,
∴OF=AF+OA=5,
∴点Q的坐标为(-5,3);

(3)设直线PQ的解析式为y=kx+b
把P(-2,5),Q(-5,3)代入y=kx+b得
|
得
|
∴y=
| 2 |
| 3 |
| 19 |
| 3 |
∴当x=0时,y=
| 19 |
| 3 |
∴直线PQ与y轴的交点Q′(0,
| 19 |
| 3 |
∴点Q(-5,3)运动到点Q′(0,
| 19 |
| 3 |
∴向右平移了5个单位长度,向上平移了
| 10 |
| 3 |
∵抛物线y=-
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
∴运动后的抛物线的顶点坐标为(4,6).
点评:本题考查了待定系数法求解析式以及与坐标轴的交点,三角形全等的判定和性质,以及动点问题,动点问题的解决关键是找到特殊分界点,进行讨论是解决问题的关键,此题综合性较强,分析过程中必须细心.

练习册系列答案
相关题目
下列条件不能判断两个直角三角形全等的是( )
| A、两条直角边分别对应相等 |
| B、斜边和一个锐角分别对应相等 |
| C、两个锐角对应相等 |
| D、斜边和一直角边分别对应相等 |
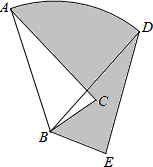 如图,在△ABC中,AB=6,将△ABC绕点B顺时针旋转60°后得到△DBE,点A经过的路径为弧AD,则图中阴影部分的面积是( )
如图,在△ABC中,AB=6,将△ABC绕点B顺时针旋转60°后得到△DBE,点A经过的路径为弧AD,则图中阴影部分的面积是( )| A、6π | B、5π | C、4π | D、3π |
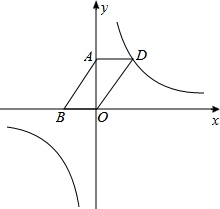 已知反比例函数y=
已知反比例函数y= 如图,双曲线y=
如图,双曲线y=