题目内容
14.在△ABC中,∠ABC=60°,AB=8,AC=7,EF为AB垂直平分线,垂足为E,交直线BC于F,则CF的长为5或3.分析 在△ABC中,已知两边和其中一边的对角,符合题意的三角形有两个,画出△ABC与△ABC′.作AD⊥BC于D,根据等腰三角形三线合一的性质得出C′D=CD.由EF为AB的垂直平分线,得出AE=BE=$\frac{1}{2}$AB=4,EF⊥AB.根据△BEF、△ABD都是含30度角的直角三角形,得到BF=2BE=8,BD=$\frac{1}{2}$AB=4,AD=$\sqrt{3}$BD=4$\sqrt{3}$,则DF=BF-BD=4.在Rt△ACD中,利用勾股定理求出CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{{7}^{2}-(4\sqrt{3})^{2}}$=1,那么C′D=CD=1,然后求出CF=CD+DF=5,或C′F=DF-C′D=3.
解答  解:如图,作AD⊥BC于D,
解:如图,作AD⊥BC于D,
∵AC=AC′=7,AD⊥BC于D,
∴C′D=CD.
∵EF为AB垂直平分线,
∴AE=BE=$\frac{1}{2}$AB=4,EF⊥AB,
∵∠ABC=60°,
∴∠BFE=90°-60°=30°,
∴BF=2BE=8.
在Rt△ABD中,∵∠ADB=90°,∠ABD=60°,
∴∠BAD=30°,
∴BD=$\frac{1}{2}$AB=4,AD=$\sqrt{3}$BD=4$\sqrt{3}$,
∴DF=BF-BD=8-4=4.
在Rt△ACD中,∵∠ADC=90°,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{{7}^{2}-(4\sqrt{3})^{2}}$=1,
∴C′D=CD=1,
∴CF=CD+DF=1+4=5或C′F=DF-C′D=4-1=3.
故答案为5或3.
点评 本题考查了含30度角的直角三角形,线段垂直平分线的性质,等腰三角形三线合一的性质,勾股定理,根据题意画出图形进行分类讨论是解题的关键.

| A. | 只能是x=-1 | |
| B. | 可能是y轴 | |
| C. | 可能在y轴右侧且在直线x=2的左侧 | |
| D. | 可能在y轴左侧且在直线x=-2的右侧 |
 如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )
如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
 已知抛物线y=x2+bx+c的顶点为M,与x轴交于点A、B,与y轴交于点C.
已知抛物线y=x2+bx+c的顶点为M,与x轴交于点A、B,与y轴交于点C.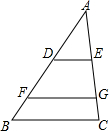 如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则CE的长为( )
如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则CE的长为( )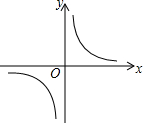 反比例函数y=$\frac{m}{x}$的图象如图所示,以下结论:
反比例函数y=$\frac{m}{x}$的图象如图所示,以下结论: