题目内容
4. 如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )
如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
分析 根据三角形外角性质可得∠3=30°+∠1,由于平行线的性质即可得到∠2=∠3=60°,即可解答.
解答 解:如图,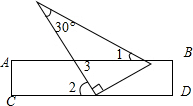
∵∠3=∠1+30°,
∵AB∥CD,
∴∠2=∠3=60°,
∴∠1=∠3-30°=60°-30°=30°.
故选D
点评 本题考查了平行线的性质,关键是根据:两直线平行,内错角相等.也利用了三角形外角性质.

练习册系列答案
相关题目
15.在平面直角坐标系中,把点P(-3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为( )
| A. | (3,2) | B. | (2,-3) | C. | (-3,-2) | D. | (3,-2) |
12. 已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
 已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )| A. | |a|<1<|b| | B. | 1<-a<b | C. | 1<|a|<b | D. | -b<a<-1 |
16.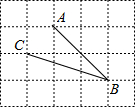 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )| A. | 2 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{1}{2}$ |
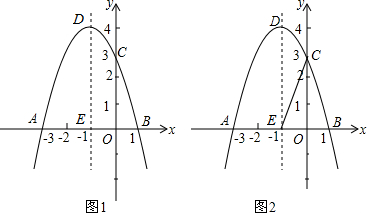
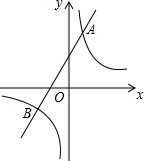 如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
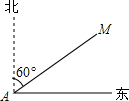 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行50$\sqrt{3}$海里可使渔船到达离灯塔距离最近的位置.
如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行50$\sqrt{3}$海里可使渔船到达离灯塔距离最近的位置.