题目内容
9．
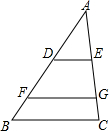如图，△ABC中，D、F在AB边上，E、G在AC边上，DE∥FG∥BC，且AD：DF：FB=3：2：1，若AG=15，则CE的长为（ ）| A． | 9 | B． | 15 | C． | 12 | D． | 6 |
分析 根据平行线分线段成比例定理得到$\frac{AF}{DB}$=$\frac{AG}{EC}$，再利用比例性质由AD：DF：FB=3：2：1得$\frac{AF}{DB}$=$\frac{5}{3}$，则$\frac{15}{EC}$=$\frac{5}{3}$，然后把AG=15代入计算即可．
解答 解：∵DE∥FG∥BC，
∴$\frac{AF}{DB}$=$\frac{AG}{EC}$，
而AD：DF：FB=3：2：1，
∴$\frac{AF}{DB}$=$\frac{5}{3}$，
∴$\frac{15}{EC}$=$\frac{5}{3}$，
∴EC=9．
故选A．
点评 本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．
练习册系列答案
相关题目
如图，网格中的四个格点组成菱形ABCD，则tan∠DBC的值为3．
4．
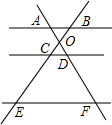如图，已知AB∥CD∥EF，直线AF与直线BE相交于点O，下列结论错误的是（ ）
如图，已知AB∥CD∥EF，直线AF与直线BE相交于点O，下列结论错误的是（ ）| A． | $\frac{AD}{DF}=\frac{BC}{CE}$ | B． | $\frac{OA}{OC}=\frac{OB}{OD}$ | C． | $\frac{CD}{EF}=\frac{OC}{OE}$ | D． | $\frac{OA}{OF}=\frac{OB}{OE}$ |
18．如图，有一块矩形纸片ABCD，AB=8，AD=6，将纸片折叠，使得AD边落在AB边上，折痕为AE，再将△AED沿DE向右翻折，AE与BC的交点为F，则△CEF的面积为（ ）
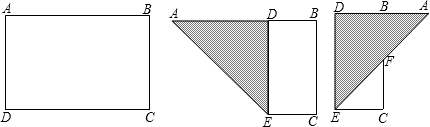
| A． | $\frac{1}{2}$ | B． | $\frac{9}{8}$ | C． | 2 | D． | 4 |
