题目内容
在△ABC中,若∠A=30°,∠B=2∠C,则∠B= .
考点:三角形内角和定理
专题:
分析:先根据三角形内角和定理得到∠A+∠B+∠C=180°,再把∠A=30°,∠B=2∠C代入可计算出∠C,则利用∠B=2∠C计算即可.
解答:解:∵∠A+∠B+∠C=180°,
而∠A=30°,∠B=2∠C,
∴30°+∠C+2∠C=180°,
∴∠C=50°,
∴∠B=2×50°=100°.
故答案为100.
而∠A=30°,∠B=2∠C,
∴30°+∠C+2∠C=180°,
∴∠C=50°,
∴∠B=2×50°=100°.
故答案为100.
点评:本题考查了三角形内角和定理:三角形内角和是180°.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,甲,乙两只小虫从A点同时出发,甲虫沿着大的半圆爬行,乙虫沿着内部的三个半圆爬行,如果两虫爬行的速度相同,则先到达B点的虫子是( )
如图,甲,乙两只小虫从A点同时出发,甲虫沿着大的半圆爬行,乙虫沿着内部的三个半圆爬行,如果两虫爬行的速度相同,则先到达B点的虫子是( )| A、甲 | B、同时到达 |
| C、乙 | D、不能确定 |
 如图,正方形ABCD内有一点D,且OA=OB=AB,则∠COD=
如图,正方形ABCD内有一点D,且OA=OB=AB,则∠COD=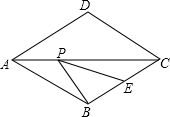 如图,在菱形ABCD中,AD=8,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为
如图,在菱形ABCD中,AD=8,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为