题目内容
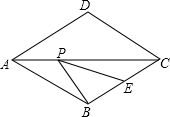 如图,在菱形ABCD中,AD=8,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为
如图,在菱形ABCD中,AD=8,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为考点:轴对称-最短路线问题,菱形的性质
专题:
分析:连接BD,DE,则DE的长即为PE+PB的最小值,再根据菱形ABCD中,∠ABC=120°得出∠BCD的度数,进而判断出△BCD是等边三角形,故△CDE是直角三角形,根据勾股定理即可得出DE的长.
解答: 解:连接BD,DE,
解:连接BD,DE,
∵四边形ABCD是菱形,
∴B、D关于直线AC对称,
∴DE的长即为PE+PB的最小值,
∵ABC=120°,
∴∠BCD=60°,
∴△BCD是等边三角形,
∵E是BC的中点,
∴DE⊥BC,CE=
BC=
×8=4,
∴DE=
=
=4
.
故答案为:4
.
 解:连接BD,DE,
解:连接BD,DE,∵四边形ABCD是菱形,
∴B、D关于直线AC对称,
∴DE的长即为PE+PB的最小值,
∵ABC=120°,
∴∠BCD=60°,
∴△BCD是等边三角形,
∵E是BC的中点,
∴DE⊥BC,CE=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=
| CD2-CE2 |
| 82-42 |
| 3 |
故答案为:4
| 3 |
点评:本题考查的是轴对称-最短路线问题,熟知菱形的性质及两点直线线段最短是解答此题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
在线段、角、两条相交直线、等边三角形、平行四边形和菱形这6种图形中,既是轴对称图形又是中心对称图形的有( )
| A、5种 | B、4种 | C、3种 | D、2种 |