题目内容
15. 如图,⊙0的半径为10cm.M是弦AB上的-个动点.且线段0M长度的最小值为8cm.则弦AB=12cm.
如图,⊙0的半径为10cm.M是弦AB上的-个动点.且线段0M长度的最小值为8cm.则弦AB=12cm.
分析 根据垂线段最短知,当OM⊥AB时,OM有最小值.根据垂径定理和勾股定理求解.
解答  解:根据垂线段最短知,当OM⊥AB时,OM有最小值,
解:根据垂线段最短知,当OM⊥AB时,OM有最小值,
此时,由垂径定理知,点M是AB的中点,
连接OA,AM=$\frac{1}{2}$AB,
由勾股定理知,OA2=OM2+AM2.
即102=82+($\frac{1}{2}$AB)2,
解得AB=12cm.
故答案为12.
点评 本题考查了垂径定理和勾股定理,根据垂线段最短知,当OM⊥AB时,OM有最小值是解题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
5.计算-3+8的值是( )
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
6.如果二次三项式ax+3x+4在实数范围内不能分解因式,那么a的取值范围是( )
| A. | 0$<a<\frac{9}{16}$,且a<0 | B. | a≠0 | C. | a$>\frac{9}{16}$ | D. | a$<\frac{3}{4}$且a≠0 |
2.在△ABC中,已知a=3$\sqrt{3}$,b=2,∠C=150°,则c=( )
| A. | 49 | B. | 7 | C. | 13 | D. | $\sqrt{13}$ |
19.如表是从左到右以及从上到下都是无限的,其中数字如图所示以一定的规律排列,100在表中共出现了6次
| 1 | 1 | 1 | 1 | 1 | … |
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 3 | 5 | 7 | 9 | |
| 1 | 4 | 7 | 10 | 13 | |
| 1 | 5 | 9 | 13 | 17 | |
| … | … |
20.下列式子是分式的是( )
| A. | $\frac{x}{3}$ | B. | $\frac{x}{x+1}$ | C. | $x+\frac{y}{2}$ | D. | 2x3 |
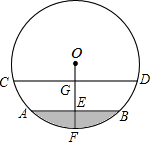 一根圆管的横截面积如图所示,圆管内原有积水的水面宽AB=40cm,水深EF=10cm,当水面上升10cm(即EG=10cm)时,水面的宽CD是多少(结果保留小数点后一位)
一根圆管的横截面积如图所示,圆管内原有积水的水面宽AB=40cm,水深EF=10cm,当水面上升10cm(即EG=10cm)时,水面的宽CD是多少(结果保留小数点后一位)