若菱形的两个内角的度数之比为1:2.较短对角线长为6.则此菱形的周长是24．题目和参考答案——青夏教育精英家教网—

题目内容

14．若菱形的两个内角的度数之比为1：2，较短对角线长为6，则此菱形的周长是24．

分析首先根据题意画出图形，然后由菱形的两个内角的度数之比为1：2，易得△ABD是等边三角形，则可求得边长，继而求得答案．

解答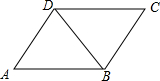解：如图，∵四边形ABCD是菱形，
∴AB=AD，∠A+∠ADC=180°，
∵菱形的两个内角的度数之比为1：2，
即∠A：∠ADC=1：2，
∴∠A=60°，
∴△ABD是等边三角形，
∵较短对角线长BD=6，
∴AB=AD=6，
∴此菱形的周长是：4×6=24．
故答案为：24．

点评此题考查了菱形的性质以及等边三角形的判定与性质．注意能证得较短对角线与两邻边组成的三角形是等边三角形是关键．

练习册系列答案

相关题目

10．若实数a、b满足ab＜0，则一次函数y=ax+b的图象可能是（　　）

5．（1）计算：（$\frac{1}{3}$）^-1-2²+（$\sqrt{3}$-tan45°）⁰；
（2）解方程组：$\left\{\begin{array}{l}x+2y=-3\\ 2x-y=4\end{array}$．

2．已知△ABC的三边长分别为4，3，6，与它相似的△DEF的最小边长为12，则△DEF的周长为（　　）

9．从标号分别为1，2，3，4，5的5张卡片中，随机抽出1张．下列事件中，必然事件是（　　）

19．$\frac{1}{2}$abc•（-$\frac{1}{2}$ab²）=-$\frac{1}{4}$a²b³c．

6．

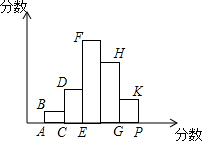如图所示，根据某班54个学生的数学成绩绘制的频数分布直方图中，各小长方形的高的比AB：CD：EF：GH：PK=1：3：7：5：2，若后两组为80分以上学生数，则80分以上学生人数是21．若80分成绩为优秀，则优秀率是38.9%．

3．

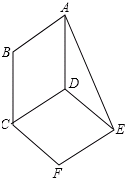如图，平行四边形ABCD与平行四边形DCFE的周长相等，且∠BAD=60°，∠F=110°，BC=6．
（1）求边CF的长；
（2）求∠DAE的度数．

4．已知等腰三角形的周长为24，腰长为x，则x的取值范围是（　　）

试题分类