题目内容
5.(1)计算:($\frac{1}{3}$)-1-22+($\sqrt{3}$-tan45°)0;(2)解方程组:$\left\{\begin{array}{l}x+2y=-3\\ 2x-y=4\end{array}$.
分析 (1)原式第一项利用负指数幂法则计算,第二项利用乘方的意义化简,最后一项利用零指数幂法则计算即可得到结果;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)原式=3-4+1=0;
(2)$\left\{\begin{array}{l}{x+2y=-3①}\\{2x-y=4②}\end{array}\right.$,
①+②×2得:5xx=5,即x=1,
把x=1代入①得:y=-2,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.在某校科技节“知识竞赛”中共进行四次比赛,甲、乙两个参赛同学,四次比赛成绩情况下表所示:
设两同学得分的平均数依次为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,得分的方差依次为$S_甲^2$,$S_乙^2$,则下列关系中完全正确的是( )
| 次数 | 第一次 | 第二次 | 第三次 | 第四次 |
| 甲 | 9.7 | 10 | 10 | 8.4 |
| 乙 | 9.2 | 10 | 9.7 | 9.2 |
| A. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,S甲2>S乙2 | B. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ | ||
| C. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,$S_甲^2>S_乙^2$ | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ |
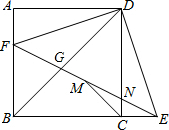 如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连结EF,DE,DF,M是FE中点,连结MC,设FE与DC相交于点N.则4个结论:①DN=DG;②△BFG∽△EDG∽△BDE;③CM垂直BD;④若MC=$\sqrt{2}$,则BF=2;正确的结论有( )
如图,正方形ABCD中,F为AB上一点,E是BC延长线上一点,且AF=EC,连结EF,DE,DF,M是FE中点,连结MC,设FE与DC相交于点N.则4个结论:①DN=DG;②△BFG∽△EDG∽△BDE;③CM垂直BD;④若MC=$\sqrt{2}$,则BF=2;正确的结论有( )