题目内容
7．计算：22016×（$\frac{1}{2}$）2017所得的结果是$\frac{1}{2}$．分析 根据同底数幂的乘法，积的乘方，可得答案．
解答 解：原式=[22016×（$\frac{1}{2}$）2016]×（$\frac{1}{2}$）
=（2×$\frac{1}{2}$）2016×$\frac{1}{2}$
=$\frac{1}{2}$，
故答案为：$\frac{1}{2}$．
点评 本题考查了积的乘方，利用同底数幂的乘法得出积的乘方是解题关键．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
17．单项式-$\frac{2{a}^{4}b{c}^{2}}{3}$的系数与次数分别是（ ）
| A． | -2，6 | B． | 2，7 | C． | -$\frac{2}{3}$，6 | D． | -$\frac{2}{3}$，7 |
2．在实数-$\frac{5}{3}$、$\frac{{\sqrt{2}}}{4}$、0.125、$\sqrt{\frac{25}{16}}$、-$\frac{π}{2}$中，分数的个数是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
如图EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD的度数．
16．如图，这些几何体都是简单几何体，请你仔细观察．
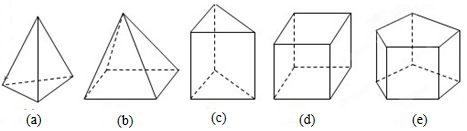
（1）认真统计每个几何体的棱数（E）、面数（F）、顶点数（V），完成表．
（2）观察表，不难发现：
①简单几何体中，每条棱都是2个面的公共边；
②在几何体c、d、e中，每个顶点处有3条棱，每条棱都有2个顶点，所以有2×E=3×V；
③简单几何体中，V、F、E之间满足后面的关系式：V+F-E=2．
（3）应用（2）题结论解答：有一个叫“正十二面体”的简单几何体，它有十二个面，每个面都是正五边形，它的每个顶点处都有相同数目的棱．则它共有30条棱，共有20个顶点，每个顶点处有3条棱．
（4）将（3）题的解题过程简要叙述在后面．
（1）认真统计每个几何体的棱数（E）、面数（F）、顶点数（V），完成表．
| 几何体 | a | b | c | d | e |
| 棱数（E） | 6 | 8 | 9 | 12 | 15 |
| 面数（F） | 4 | 5 | 5 | 6 | 7 |
| 顶点数（V） | 4 | 5 | 6 | 8 | 10 |
①简单几何体中，每条棱都是2个面的公共边；
②在几何体c、d、e中，每个顶点处有3条棱，每条棱都有2个顶点，所以有2×E=3×V；
③简单几何体中，V、F、E之间满足后面的关系式：V+F-E=2．
（3）应用（2）题结论解答：有一个叫“正十二面体”的简单几何体，它有十二个面，每个面都是正五边形，它的每个顶点处都有相同数目的棱．则它共有30条棱，共有20个顶点，每个顶点处有3条棱．
（4）将（3）题的解题过程简要叙述在后面．