题目内容
8.化简求值.已知:A=-4a3+a-a2+1,B=-2a3+7a2-a,求代数式A-3(B-A)的值,其中a=-$\frac{1}{2}$.
分析 把A与B代入原式计算得到最简结果,把a的值代入计算即可求出值.
解答 解:∵A=-4a3+a-a2+1,B=-2a3+7a2-a,
∴A-3(B-A)=A-3B+3A=4A-3B=-16a3+4a-4a2+4+6a3-21a2+3a=-10a3-25a2+7a+4,
当a=-$\frac{1}{2}$时,原式=$\frac{5}{4}$-$\frac{25}{4}$-$\frac{7}{2}$+4=-$\frac{9}{2}$.
点评 此题考查了整式的加减-化简求值,熟练掌握去括号法则与合并同类项法则是解本题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
16.如图,这些几何体都是简单几何体,请你仔细观察.
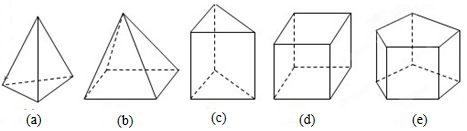
(1)认真统计每个几何体的棱数(E)、面数(F)、顶点数(V),完成表.
(2)观察表,不难发现:
①简单几何体中,每条棱都是2个面的公共边;
②在几何体c、d、e中,每个顶点处有3条棱,每条棱都有2个顶点,所以有2×E=3×V;
③简单几何体中,V、F、E之间满足后面的关系式:V+F-E=2.
(3)应用(2)题结论解答:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.则它共有30条棱,共有20个顶点,每个顶点处有3条棱.
(4)将(3)题的解题过程简要叙述在后面.

(1)认真统计每个几何体的棱数(E)、面数(F)、顶点数(V),完成表.
| 几何体 | a | b | c | d | e |
| 棱数(E) | 6 | 8 | 9 | 12 | 15 |
| 面数(F) | 4 | 5 | 5 | 6 | 7 |
| 顶点数(V) | 4 | 5 | 6 | 8 | 10 |
①简单几何体中,每条棱都是2个面的公共边;
②在几何体c、d、e中,每个顶点处有3条棱,每条棱都有2个顶点,所以有2×E=3×V;
③简单几何体中,V、F、E之间满足后面的关系式:V+F-E=2.
(3)应用(2)题结论解答:有一个叫“正十二面体”的简单几何体,它有十二个面,每个面都是正五边形,它的每个顶点处都有相同数目的棱.则它共有30条棱,共有20个顶点,每个顶点处有3条棱.
(4)将(3)题的解题过程简要叙述在后面.
20.下列一元二次方程有两个相等实数根的是( )
| A. | 2x2-x-1=0 | B. | x2-4x+4=0 | C. | 4x2-2x-3=0 | D. | x2+6x=0 |
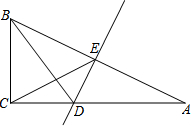 如图,在Rt△ABC中,∠C=Rt∠,AB的垂直平分线交AC于点D,交AB于点E,BD平分∠ABC.
如图,在Rt△ABC中,∠C=Rt∠,AB的垂直平分线交AC于点D,交AB于点E,BD平分∠ABC. 如图,已知直线AB∥CD,∠1=50°,那么∠2=130°.
如图,已知直线AB∥CD,∠1=50°,那么∠2=130°.