题目内容
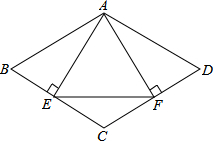 如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则的△AEF的面积是( )
如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则的△AEF的面积是( )A、4
| ||
B、3
| ||
C、2
| ||
D、
|
考点:菱形的性质
专题:
分析:首先利用菱形的性质及等边三角形的判定可得判断出△AEF是等边三角形,再根据三角函数计算出AE=EF的值,再过A作AM⊥EF,再进一步利用三角函数计算出AM的值,即可算出三角形的面积.
解答: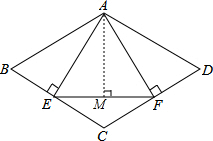 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴BC=CD,∠B=∠D=60°,
∵AE⊥BC,AF⊥CD,
∴BC×AE=CD×AF,∠BAE=∠DAF=30°,
∴AE=AF,
∵∠B=60°,
∴∠BAD=120°,
∴∠EAF=120°-30°-30°=60°,
∴△AEF是等边三角形,
∴AE=EF,∠AEF=60°,
∵AB=4,
∴AE=2
,
∴EF=AE=2
,
过A作AM⊥EF,
∴AM=AE•sin60°=3,
∴△AEF的面积是:
EF•AM=
×2
×3=3
.
故选:B.
 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,∴BC=CD,∠B=∠D=60°,
∵AE⊥BC,AF⊥CD,
∴BC×AE=CD×AF,∠BAE=∠DAF=30°,
∴AE=AF,
∵∠B=60°,
∴∠BAD=120°,
∴∠EAF=120°-30°-30°=60°,
∴△AEF是等边三角形,
∴AE=EF,∠AEF=60°,
∵AB=4,
∴AE=2
| 3 |
∴EF=AE=2
| 3 |
过A作AM⊥EF,
∴AM=AE•sin60°=3,
∴△AEF的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故选:B.
点评:此题考查菱形的性质,等边三角形的判定及三角函数的运用.关键是掌握菱形的性质,证明△AEF是等边三角形.

练习册系列答案
相关题目
 有理数a,b在数轴上的位置如图所示,那么下列式子中不一定成立的是( )
有理数a,b在数轴上的位置如图所示,那么下列式子中不一定成立的是( )| A、a>b | ||
| B、b-a<0 | ||
C、
| ||
| D、|a|≥|b| |
已知反比例函数y=
的图象上有A(x1,y1)、B(x2,y2)两点,当x1<x2<0时,y1<y2.则m的取值范围是( )
| 2-5m |
| x |
| A、m<0 | ||
| B、m>0 | ||
C、m<
| ||
D、m>
|
 DE为△ABC的中位线,连接BE,且BE=BC,延长DE到点F,使EF=BE,连接CF,BF.
DE为△ABC的中位线,连接BE,且BE=BC,延长DE到点F,使EF=BE,连接CF,BF. 如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,反比例函数y=
如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,反比例函数y= 如图,Rt△ABC中,∠C=90°,AB=8cm,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向往返运动,设E点的运动时间为ts(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为
如图,Rt△ABC中,∠C=90°,AB=8cm,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向往返运动,设E点的运动时间为ts(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为 已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.