题目内容
已知反比例函数y=
的图象上有A（x1，y1）、B（x2，y2）两点，当x1＜x2＜0时，y1＜y2．则m的取值范围是（ ）
| 2-5m |
| x |
| A、m＜0 | ||
| B、m＞0 | ||
C、m＜
| ||
D、m＞
|
考点：二次函数图象上点的坐标特征
专题：计算题
分析：根据反比例函数图象上点的坐标特征得x1=
，x2=
，而x1＜x2＜0时，y1＜y2，则2-5m＜0，然后解不等式即可．
| 2-5m |
| y1 |
| 2-5m |
| y2 |
解答：解：∵反比例函数y=
的图象上有A（x1，y1）、B（x2，y2），
∴x1=
，x2=
，
∵x1＜x2＜0时，y1＜y2，
∴2-5m＜0，
∴m＞
．
故选D．
| 2-5m |
| x |
∴x1=
| 2-5m |
| y1 |
| 2-5m |
| y2 |
∵x1＜x2＜0时，y1＜y2，
∴2-5m＜0，
∴m＞
| 2 |
| 5 |
故选D．
点评：本题考查了反比例函数图象上点的坐标特征：反比例函数图象上点的坐标满足其解析式．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
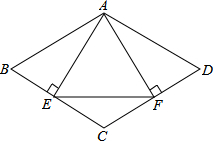如图，菱形ABCD中，AB=4，∠B=60°，AE⊥BC，AF⊥CD，垂足分别为E，F，连接EF，则的△AEF的面积是（ ）A、4
| ||
B、3
| ||
C、2
| ||
D、
|
如图，在一长方形内有对角线长分别为2，3的菱形以及半径为1的圆，若一点随机落在这两个图形内，则概率较大的是（ ）| A、落在菱形内 | B、落在圆内 |
| C、无法判断 | D、一样大 |
如图，已知抛物线y1=-2x2+2与直线y2=2x+2交于A、B两点将不等式组
的解集表示在数轴上，正确的是（ ）
|
A、 |
B、 |
C、 |
D、 |
下列计算正确的是（ ）
| A、（x-8y）（x-y）=x2-9xy+8y2 |
| B、（a-1）2=a2-1 |
| C、-x（x2+x-1）=-x3+x2-x |
| D、（x+y）（x2+xy+y2）=x3+y3 |
下列式子中，是一元一次方程的是（ ）
| A、x-7 | ||
B、
| ||
| C、2x=0 | ||
| D、2x-y=1 |