题目内容
 已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.(1)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(2)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
考点:相似三角形的判定与性质,全等三角形的判定与性质
专题:
分析:(1)如图,证明△BGE∽△ABE.得到
=(
)2;求出AE的长度,即可解决问题.
(2)如图,证明∠BAE=30°;证明△ADE′≌△AB′E′,得到∠DAE′=∠B′AE′=∠BAE=30°;得到AB′与AE在同一直线上;证明△BAG≌△HAG,得到S四边形GHE′B′=S△AB′E′-S△AGH=S△ABE-S△ABG=S△BGE,即可解决问题.
| S△BGE |
| S△ABE |
| BE |
| AE |
(2)如图,证明∠BAE=30°;证明△ADE′≌△AB′E′,得到∠DAE′=∠B′AE′=∠BAE=30°;得到AB′与AE在同一直线上;证明△BAG≌△HAG,得到S四边形GHE′B′=S△AB′E′-S△AGH=S△ABE-S△ABG=S△BGE,即可解决问题.
解答: 解:(1)如图,∵正方形面积为3,
解:(1)如图,∵正方形面积为3,
∴AB=
.
在△BGE与△ABE中,
∵∠GBE=∠BAE,∠EGB=∠EBA=90°,
∴△BGE∽△ABE.
∴
=(
)2.
又∵BE=1,
∴AE2=AB2+BE2=3+1=4.
∴AE=2;
∴S△BGE=
•S△ABE=
×
=
.
(2)没有变化. 理由如下:
∵AB=
,BE=1,
∴tan∠BAE=
=
.
∴∠BAE=30°.
在△ADE′与△AB′E′中,
,
∴△ADE′≌△AB′E′(HL),
∴∠DAE′=∠B′AE′=∠BAE=30°.
∴AB′与AE在同一直线上,
即BF与AB′的交点是G.
设BF与AE′的交点为H,
则∠BAG=∠HAG=30°;
在△BAG与△HAG中,
,
∴△BAG≌△HAG(ASA),
∴S四边形GHE′B′=S△AB′E′-S△AGH=S△ABE-S△ABG=S△BGE,
∴△ABE在旋转前后与△BCF重叠部分的面积没有变化.
 解:(1)如图,∵正方形面积为3,
解:(1)如图,∵正方形面积为3,∴AB=
| 3 |
在△BGE与△ABE中,
∵∠GBE=∠BAE,∠EGB=∠EBA=90°,
∴△BGE∽△ABE.
∴
| S△BGE |
| S△ABE |
| BE |
| AE |
又∵BE=1,
∴AE2=AB2+BE2=3+1=4.
∴AE=2;
∴S△BGE=
| BE2 |
| AE2 |
| 1 |
| 4 |
| ||
| 2 |
| ||
| 8 |
(2)没有变化. 理由如下:
∵AB=
| 3 |
∴tan∠BAE=
| 1 | ||
|
| ||
| 3 |
∴∠BAE=30°.
在△ADE′与△AB′E′中,
|
∴△ADE′≌△AB′E′(HL),
∴∠DAE′=∠B′AE′=∠BAE=30°.
∴AB′与AE在同一直线上,
即BF与AB′的交点是G.
设BF与AE′的交点为H,
则∠BAG=∠HAG=30°;
在△BAG与△HAG中,
|
∴△BAG≌△HAG(ASA),
∴S四边形GHE′B′=S△AB′E′-S△AGH=S△ABE-S△ABG=S△BGE,
∴△ABE在旋转前后与△BCF重叠部分的面积没有变化.
点评:该题主要考查了全等三角形的判定及其性质、相似三角形的判定及其性质等几何知识点及其应用问题;解题的关键是认真观察图形,找出图形中隐含的等量关系或全等关系.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
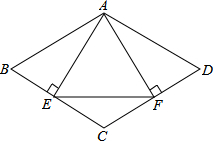 如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则的△AEF的面积是( )
如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则的△AEF的面积是( )A、4
| ||
B、3
| ||
C、2
| ||
D、
|
 如图,在一长方形内有对角线长分别为2,3的菱形以及半径为1的圆,若一点随机落在这两个图形内,则概率较大的是( )
如图,在一长方形内有对角线长分别为2,3的菱形以及半径为1的圆,若一点随机落在这两个图形内,则概率较大的是( )| A、落在菱形内 | B、落在圆内 |
| C、无法判断 | D、一样大 |
下列计算正确的是( )
| A、(x-8y)(x-y)=x2-9xy+8y2 |
| B、(a-1)2=a2-1 |
| C、-x(x2+x-1)=-x3+x2-x |
| D、(x+y)(x2+xy+y2)=x3+y3 |
 如图,在△ABC中,∠ABC=∠C,BD平分∠ABC,∠A=36°,则∠BDC=
如图,在△ABC中,∠ABC=∠C,BD平分∠ABC,∠A=36°,则∠BDC=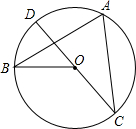 如图,CD是⊙O的直径,A,B是⊙O上任意两点,设∠BAC=y,∠BOD=x,则y与x之间的函数关系式是
如图,CD是⊙O的直径,A,B是⊙O上任意两点,设∠BAC=y,∠BOD=x,则y与x之间的函数关系式是



