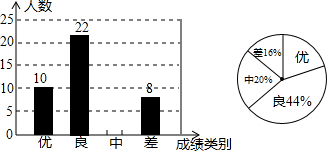
��Ŀ����
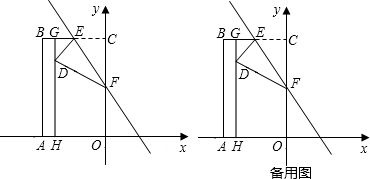
2����ͼ��������OABC��ƽ��ֱ������ϵ�ڣ�OΪ����ԭ�㣩����A��x���ϣ���C��y���ϣ���B������Ϊ��-2��2$\sqrt{3}$������E��BC���е㣬��H��OA�ϣ���AH=$\frac{1}{2}$������H��ƽ����y���HG��EB���ڵ�G���ֽ��������۵���ʹ����C����HG�ϣ�����HG�ϵĵ�D�غϣ��ۺ�ΪEF�����ۺ۽�y���ڵ�F��������1����CEF�Ķ����͵�D�����ꣻ
��2���ۺ�EF����ֱ�ߵĺ�������ʽ��
��3����y�����Ƿ���ڵ�Mʹ��S��EFD=S��EFM�������ڣ������M�����꣬�������ڣ���˵�����ɣ�
��4������P��ֱ��EF�ϣ�����PFDΪ����������ʱ���������������ĵ�P�м������������P�����꣨����д�������̣���
���� ��1���������������EC=EB=1��������ԳƵ����ʿ������ED=1���������Ǻ���ֵ�����GED�Ķ������Ӷ����������CEF�Ķ��������ù��ɶ������DG��ֵ����������D������ꣻ
��2���������Ǻ���ֵ���CF��ֵ���Ӷ����F�����꣬���ֱ��EF�Ľ���ʽ��ֱ�����ô���ϵ������������ʽ�Ϳ����ˣ�
��3����D��DN��EF�����ݡ�EDF�ա�CEF�������CΪ��������������һ�㣬��M��F���·�ʱ����M��MK��EF�ڵ�K�����MK��������⣻
��4����ͼ2�����ݵ��������ε����������P�����꣬�������ľ��빫ʽ�Ϳ��������P�����꣮
��� �⣺��1����E��BC���е㣬
��EC=EB=$\frac{2}{2}$=1��
�ߡ�FCE���FDE����ֱ��EF�Գƣ�
���FCE�ա�FDE��
��ED=EC=1����FCE=��FDE=90�㣬DF=CF��
��AH=$\frac{1}{2}$��
��EG=EB-AH=1-$\frac{1}{2}$=$\frac{1}{2}$��
��cos��GED=$\frac{EG}{ED}$=$\frac{1}{2}$��
���GED=60�㣮
���DEC=180��-60��=120�㣮
�ߡ�DEF=��CEF
���CEF=$\frac{120}{2}$=60�㣮
��Rt��GED�У��ɹ��ɶ����ã�
DG2=ED2-EG2=1-$\frac{1}{4}$=$\frac{3}{4}$
��DG=$\frac{\sqrt{3}}{2}$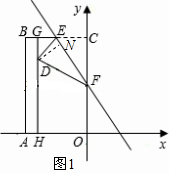
DH=AB-DG=2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$
OH=OA-AH=2-$\frac{1}{2}$=$\frac{3}{2}$
��D��-$\frac{3}{2}$��$\frac{3\sqrt{3}}{2}$��
��2���ߡ�CEF�T60��
��CF=ECtan60��=$\sqrt{3}$
��OF=OC-CF=2$\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$
��F��0��$\sqrt{3}$����E��-1��2$\sqrt{3}$��
��EF����ֱ�ߵĺ�������ʽΪy=kx+b����ͼ��$\left\{\begin{array}{l}{\sqrt{3}=b}\\{2\sqrt{3}=-k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=\sqrt{3}}\end{array}\right.$
��EF����ֱ�ߵĺ�������ʽΪ��y=-$\sqrt{3}$x+$\sqrt{3}$��
��3�����ڣ�
��D��DN��EF����DN=$\frac{\sqrt{3}}{2}$��
�ߡ�EDF�ա�CEF��
��CΪ��������������һ�㣬��M��0��2$\sqrt{3}$����
��M��F���·�ʱ����M��MK��EF�ڵ�K��
��MK=$\frac{\sqrt{3}}{2}$����2=��3=30�㣬
��MF=$\sqrt{3}$����ʱM��O�غϣ���M��0��0����
������������M�������ǣ�0��0����M��0��2$\sqrt{3}$����
��4����DF=CF=$\sqrt{3}$��P��ֱ��EF�ϣ�
�൱��PFDΪ����������ʱ�����������������
��a��P1F=DF=$\sqrt{3}$��
����P1��t��-$\sqrt{3}$t+$\sqrt{3}$������
P1F2=3
���������ľ��빫ʽΪ��
��t-0��2+��-$\sqrt{3}$t+$\sqrt{3}$-$\sqrt{3}$��2=3
��t2+3t2=3
��t2=$\frac{3}{4}$��
��t1=-$\frac{\sqrt{3}}{2}$��t2=$\frac{\sqrt{3}}{2}$
��P1��-$\frac{\sqrt{3}}{2}$��$\frac{3}{2}$+$\sqrt{3}$���� P3��$\frac{\sqrt{3}}{2}$��-$\frac{3}{2}$+$\sqrt{3}$��
��b�� PD=DF=$\sqrt{3}$ʱ��
����P��t��-$\sqrt{3}$t+$\sqrt{3}$����ע��D��-$\frac{3}{2}$��$\frac{3\sqrt{3}}{2}$������
PD2=3
�ࣨt+$\frac{3}{2}$��2+��-$\sqrt{3}$t+$\sqrt{3}$-$\frac{3\sqrt{3}}{2}$��2=3
��t2+3t+$\frac{9}{4}$+3t2+3t+$\frac{3}{4}$=3
��4t2+6t=0
��t1=0��t2=-$\frac{3}{2}$
��t1=0��ӦF�㣬��ʱ�����������Σ�����ȥ��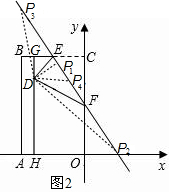
��P3��-$\frac{3}{2}$��$\frac{5\sqrt{3}}{2}$��
��c���� PD=PF
����P��t��-$\sqrt{3}$t+$\sqrt{3}$����ע��D��-$\frac{3}{2}$��$\frac{3\sqrt{3}}{2}$����F��0��$\sqrt{3}$������
PD2=PF2
�ࣨt+$\frac{3}{2}$��2+��-$\frac{\sqrt{3}}{3}$t+$\sqrt{3}$-$\frac{3\sqrt{3}}{2}$��2=��t-0��2+��-$\sqrt{3}$t+$\sqrt{3}$-$\sqrt{3}$��2��
��t2+3t+$\frac{9}{4}$+3t2+3t+$\frac{3}{4}$=t2+3t2
��6t+3=0
��t=-$\frac{1}{2}$
��P4��-$\frac{1}{2}$��$\frac{3\sqrt{3}}{2}$����
�����������ĵ�P��4�����ֱ���P1��-$\frac{\sqrt{3}}{2}$��$\frac{3}{2}$+$\sqrt{3}$���� P2��$\frac{\sqrt{3}}{2}$��-$\frac{3}{2}$+$\sqrt{3}$����P3��-$\frac{3}{2}$��$\frac{5\sqrt{3}}{2}$����P4��-$\frac{1}{2}$��$\frac{3\sqrt{3}}{2}$����
���� ������һ��һ�κ������ۺ����⣬��������ԳƵ����ʵ����ã�����ϵ������һ�κ����Ľ���ʽ�����ü������������ε����ʵ����ã��ڽ��ʱ���ֱ��EF�Ľ���ʽʱ�ؼ���

 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д� ��ͼ����ABC�У�AB=AC����A=36�㣬��ABC�͡�ACB��ƽ���߽��ڵ�F����ͼ�й��е��������Σ�������
��ͼ����ABC�У�AB=AC����A=36�㣬��ABC�͡�ACB��ƽ���߽��ڵ�F����ͼ�й��е��������Σ�������| A�� | 7�� | B�� | 8�� | C�� | 9�� | D�� | 10�� |
| A�� | ����2�� | B�� | ��С2�� | C�� | ���� | D�� | ��С3�� |
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{5}{6}$ |
 ��ͼ��ֱ��a��b��c�����ཻ��A��B��C���㣬��ͼ����6�ԶԶ��ǣ���12��ͬλ�ǣ���6���ڴ��ǣ���6��ͬ���ڽǣ�
��ͼ��ֱ��a��b��c�����ཻ��A��B��C���㣬��ͼ����6�ԶԶ��ǣ���12��ͬλ�ǣ���6���ڴ��ǣ���6��ͬ���ڽǣ�