题目内容
13.分解因式:x2y-9y=y(x+3)(x-3);计算:(-$\frac{1}{3}$)-2+3$\sqrt{\frac{1}{3}}$-$\sqrt{12}$=9-$\sqrt{3}$.分析 原式提取公因式,再利用平方差公式分解即可;原式利用负指数幂法则,以及二次根式性质计算即可得到结果.
解答 解:原式=y(x2-9)=y(x+3)(x-3);
原式=9+3×$\frac{\sqrt{3}}{3}$-2$\sqrt{3}$=9-$\sqrt{3}$.
故答案为:y(x+3)(x-3);9-$\sqrt{3}$.
点评 此题考查了提公因式法与公式法的综合运用,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
4.已知点A(1,m)与点(3,n)都在反比例函数y=-$\frac{3}{x}$的图象上,则m与n的大小关系是( )
| A. | m<n | B. | m>n | C. | m=n | D. | 不能确定 |
5.校篮球队所买10双运动鞋的尺码统计如表:
则这10双运动鞋尺码的众数和中位数分别为( )
| 尺码(cm) | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量(双) | 1 | 1 | 2 | 4 | 2 |
| A. | 4cm,26cm | B. | 4cm,26.5cm | C. | 26.5cm,26.5cm | D. | 26.5cm,26cm |
 如图,?ABCD的周长为20,对角线AC,BD交于点O,OE⊥AC交AD于点E,则△CDE的周长为10.
如图,?ABCD的周长为20,对角线AC,BD交于点O,OE⊥AC交AD于点E,则△CDE的周长为10.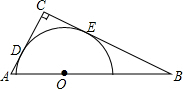 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则AD的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则AD的长为( )