题目内容
2.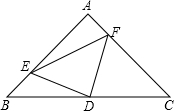 如图,在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,AE=CF.求证:△DEF是等腰直角三角形.
如图,在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,AE=CF.求证:△DEF是等腰直角三角形.
分析 连接AD,由等腰直角三角形的性质得出AD=$\frac{1}{2}$BC=CD=BD,∠C=∠DAE=45°,由SAS证明证明△ADE≌△CDF,可得DF=DE,∠CDF=∠ADE,即可求得∠EDF=90°,即可得出结论.
解答 证明:连接AD,如图所示: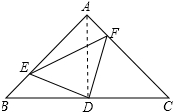
∵D是BC的中点,∠BAC=90°,AB=AC,
∴AD=$\frac{1}{2}$BC=CD=BD,∠C=∠DAE=45°,∠ADC=90°,
在△ADE和△CDF中,
$\left\{\begin{array}{l}{AD=CD}&{\;}\\{∠DAE=∠C}&{\;}\\{AE=CF}&{\;}\end{array}\right.$,
∴△ADE≌△CDF(SAS)
∴DE=DF,∠CDF=∠ADE,
∵∠ADF+∠CDF=∠ADC=90°,
∴∠ADF+∠ADE=90°,
即∠EDF=90°,
∴△DEF是等腰直角三角形.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的性质;熟练掌握等腰直角三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
8.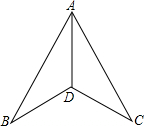 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )
 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )| A. | BD=DC,AB=AC | B. | ∠ADB=∠ADC,AB=AC | C. | ∠B=∠C,∠BAD=∠CAD | D. | ∠ADB=∠ADC,BD=CD |
 如图,在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F.求证:CD=DF.
如图,在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F.求证:CD=DF. 如图.已知点B、C、D在同一条直线上.△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,
如图.已知点B、C、D在同一条直线上.△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H, 如图,等边△ABC的边长为12cm,D为AC边上一动点,E为AB延长线上一动点,DE交CB于P,点P为DE中点.
如图,等边△ABC的边长为12cm,D为AC边上一动点,E为AB延长线上一动点,DE交CB于P,点P为DE中点. 如图所示,△ABC和△CDE是等边三角形,E是AC延长线上一点,M是AD的中点,N是BE的中点.试说明:△CMN是等边三角形.
如图所示,△ABC和△CDE是等边三角形,E是AC延长线上一点,M是AD的中点,N是BE的中点.试说明:△CMN是等边三角形.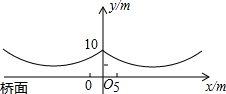 如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称.
如图所示,桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,左边的一条抛物线可以用y=$\frac{9}{400}$x2+$\frac{9}{10}$x+10表示,而且左、右两条抛物线关于y轴对称.