题目内容
12.已知关于x的一元二次方程x2-(2k+1)+k2+2k=0有两个实数根x1,x2.(1)当x1=x2,求实数k的值;
(2)是否存在实数k使得x1•x2-x12-x22≥0成立?若存在,请求出k的值;若不存在,请说明理由.
分析 (1)根据题意得出△=0,得出关于k的方程,求出方程的解即可;
(2)假设存在,得出关于k的不等式,求出不等式的解集即可.
解答 解:(1)∵关于x的一元二次方程x2-(2k+1)+k2+2k=0有两个实数根x1,x2.x1=x2,
∴△=0,
即[-(2k+1)]2-4×1×(k2+2k)=0,
解得:k=$\frac{1}{4}$;
(2)根据根与系数的关系得:x1+x2=2k+1,x1•x2=k2+2k,
假设存在实数k使得x1•x2-x12-x22≥0成立,
x1•x2-(x12+x22)≥0,
x1•x2-[(x1+x2)2-2x1•x2]≥0,
代入得:(k2+2k)-[(2k+1)2-2(k2+2k)]≥0,
即-(k-1)2≥0,
解得:k=1,
所以存在实数k使得x1•x2-x12-x22≥0成立,k的值是1.
点评 本题考查了解不等式,根与系数的关系,根的判别式的应用,能熟记根与系数的关系和根的判别式的内容是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.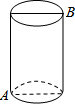 如图,有一圆柱体,高9cm,底面周长24cm,在圆柱的下底面点A处有一蜘蛛,它想吃到上底面与点A相对的B处的苍蝇,需要爬行的最短路程是( )
如图,有一圆柱体,高9cm,底面周长24cm,在圆柱的下底面点A处有一蜘蛛,它想吃到上底面与点A相对的B处的苍蝇,需要爬行的最短路程是( )
 如图,有一圆柱体,高9cm,底面周长24cm,在圆柱的下底面点A处有一蜘蛛,它想吃到上底面与点A相对的B处的苍蝇,需要爬行的最短路程是( )
如图,有一圆柱体,高9cm,底面周长24cm,在圆柱的下底面点A处有一蜘蛛,它想吃到上底面与点A相对的B处的苍蝇,需要爬行的最短路程是( )| A. | 9cm | B. | 10cm | C. | 12cm | D. | 15cm |
7.下列各图中,是中心对称图形的为( )
| A. |  | B. |  | C. |  | D. |  |
1.已知x1、x2是一元二次方程x2+2ax+b=0的两个根,且x1+x2=-3,x1x2=-1,则a、b的值分别是( )
| A. | a=-3,b=1 | B. | a=3,b=1 | C. | a=$\frac{3}{2}$,b=-1 | D. | a=-$\frac{3}{2}$,b=1 |
2.(1)填表
(2)根据发现的规律填空
①已知$\root{3}{3}$=1.442,则$\root{3}{3000}$=14.42,$\root{3}{0.003}$=0.1442
②已知$\root{3}{343}$=7,则$\root{3}{0.000343}$=0.07.
| a | 0.000001 | 0.001 | 1 | 1000 | 1000000 |
| $\root{3}{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
①已知$\root{3}{3}$=1.442,则$\root{3}{3000}$=14.42,$\root{3}{0.003}$=0.1442
②已知$\root{3}{343}$=7,则$\root{3}{0.000343}$=0.07.
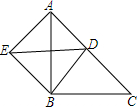 已知:如图,△ABC中,AB=BC,∠ABC=90°,点D在AC上,∠DBE=90°,BE=BD.求证:CD=AE.
已知:如图,△ABC中,AB=BC,∠ABC=90°,点D在AC上,∠DBE=90°,BE=BD.求证:CD=AE.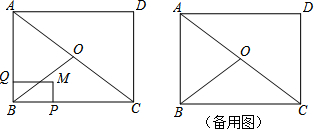
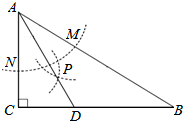 如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )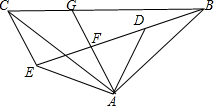 如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,下面结论正确的是①③④(填序号).
如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,下面结论正确的是①③④(填序号).