题目内容
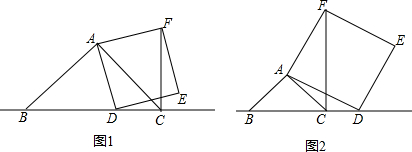
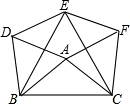 如图,以△ABC的三边为边,在BC边的同侧作等边△DBA,△EBC,△FAC.
如图,以△ABC的三边为边,在BC边的同侧作等边△DBA,△EBC,△FAC.(1)试说明四边形AFED是平行四边形;
(2)当△ABC满足什么条件时,四边形AFED是矩形,说明理由;
(3)当△ABC满足什么条件时,四边形AFED是正方形?
(4)当△ABC满足什么条件时,四边形AFED不存在?
考点:正方形的判定,全等三角形的判定与性质,平行四边形的判定,矩形的判定
专题:
分析:(1)由△DBA,△EBC,△FAC都是等边三角形,根据等边三角形的性质得出AB=DB,BC=BE,AC=AF,∠ABD=∠EBC=60°,那么∠DBE=∠ABC.利用SAS证明△DBE≌△ABC,根据全等三角形对应边相等得出DE=AC,等量代换得到DE=AF,同理DA=EF,根据两组对边分别相等的四边形是平行四边形即可得出四边形AFED是平行四边形;
(2)当∠BAC=150°时,四边形ADEF是矩形.可先根据周角的定义求出∠DAF=360°-∠DAB-∠BAC-∠CAF=90°,再根据有一个角是直角的平行四边形是矩形即可证明四边形AFED是矩形;
(3)当△ABC是顶角为150°的等腰三角形时,四边形ADEF是正方形.根据有一组邻边相等的矩形是正方形即可证明四边形AFED是正方形;
(4)当∠BAC=60°时,∠DAF=180°,此时D、A、F三点在同一条直线上,以A,D,E,F为顶点的四边形就不存在.
(2)当∠BAC=150°时,四边形ADEF是矩形.可先根据周角的定义求出∠DAF=360°-∠DAB-∠BAC-∠CAF=90°,再根据有一个角是直角的平行四边形是矩形即可证明四边形AFED是矩形;
(3)当△ABC是顶角为150°的等腰三角形时,四边形ADEF是正方形.根据有一组邻边相等的矩形是正方形即可证明四边形AFED是正方形;
(4)当∠BAC=60°时,∠DAF=180°,此时D、A、F三点在同一条直线上,以A,D,E,F为顶点的四边形就不存在.
解答:解:(1)∵△ABD,△BCE,△FAC是等边三角形,
∴AB=DB,BC=BE,AC=AF,∠ABD=∠EBC=60°,
∴∠DBE=∠ABC.
在△BDE和△BAC中,
,
∴△DBE≌ABC(SAS),
∴DE=AC,
∴DE=AF.
同理可得DA=EF,
∴四边形AFED是平行四边形;
(2)当∠BAC=150°时,四边形ADEF是矩形.理由如下:
∵∠DAF=360°-∠DAB-∠BAC-∠CAF=360°-60°-150°-60°=90°,
∴?AFED是矩形;
(3)当△ABC是顶角为150°的等腰三角形时,四边形ADEF是正方形.理由如下:
由(2)可知,当∠BAC=150°时,四边形ADEF是矩形,
∵AB=AC,
∴矩形AFED是正方形;
(4)当∠BAC=60°时,∠DAF=180°,
此时D、A、F三点在同一条直线上,以A,D,E,F为顶点的四边形就不存在.
∴AB=DB,BC=BE,AC=AF,∠ABD=∠EBC=60°,
∴∠DBE=∠ABC.
在△BDE和△BAC中,
|
∴△DBE≌ABC(SAS),
∴DE=AC,
∴DE=AF.
同理可得DA=EF,
∴四边形AFED是平行四边形;
(2)当∠BAC=150°时,四边形ADEF是矩形.理由如下:
∵∠DAF=360°-∠DAB-∠BAC-∠CAF=360°-60°-150°-60°=90°,
∴?AFED是矩形;
(3)当△ABC是顶角为150°的等腰三角形时,四边形ADEF是正方形.理由如下:
由(2)可知,当∠BAC=150°时,四边形ADEF是矩形,
∵AB=AC,
∴矩形AFED是正方形;
(4)当∠BAC=60°时,∠DAF=180°,
此时D、A、F三点在同一条直线上,以A,D,E,F为顶点的四边形就不存在.
点评:本题考查了等边三角形的性质,全等三角形的判定与性质,平行四边形、矩形、正方形的判定等知识,熟练掌握相关的定理是解题关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 如图,一条公路转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=OC=600米,E为弧CD上一点,且OE⊥CD,垂足为F,则这段弯路的长度为( )
如图,一条公路转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=OC=600米,E为弧CD上一点,且OE⊥CD,垂足为F,则这段弯路的长度为( )| A、200π米 |
| B、100π米 |
| C、400π米 |
| D、300π米 |
抛物线y=-x2-2x+3与坐标轴的交点个数是( )
| A、0 | B、1 | C、2 | D、3 |
函数y=-x2+px+q的图象与x轴交于(a,0),(b,0)两点,若a>1>b,则( )
| A、p+q>1 | B、p+q=1 |
| C、p+q<1 | D、pq>0 |
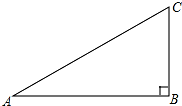 如图,在直角三角形ABC中,∠ABC=90°
如图,在直角三角形ABC中,∠ABC=90°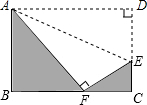 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在ABC边上F点处,已知CE=4cm,AB=9cm,则矩形ABCD的面积为
如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在ABC边上F点处,已知CE=4cm,AB=9cm,则矩形ABCD的面积为