题目内容
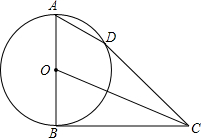如图，已知AB是⊙O的直径，点D在⊙O上，C是⊙O外一点．若AD∥OC，直线BC与⊙O相交，判断直线CD与⊙O的位置关系，并说明理由．考点：切线的判定
专题：
分析：如图，作辅助线；证明△OBC≌△ODC，得到∠ODC=∠OBC；证明∠OBC=90°，即可解决问题．
解答：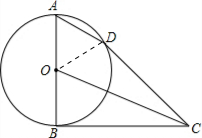
证明：如图，连接OD；
∵OA=OD，
∴∠A=∠ODA；
∵AD∥OC，
∴∠BOC=∠A、∠DOC=∠ODA，
∴∠BOC=∠DOC；在△OBC与△ODC中，
，
∴△OBC≌△ODC（SAS），
∴∠ODC=∠OBC；
∵BC与圆交，∠OBC≠90°
∴∠ODC≠90°
∴CD与⊙O相交．
证明：如图，连接OD；∵OA=OD，
∴∠A=∠ODA；
∵AD∥OC，
∴∠BOC=∠A、∠DOC=∠ODA，
∴∠BOC=∠DOC；在△OBC与△ODC中，
|
∴△OBC≌△ODC（SAS），
∴∠ODC=∠OBC；
∵BC与圆交，∠OBC≠90°
∴∠ODC≠90°
∴CD与⊙O相交．
点评：该题主要考查了圆的切线的判定及其性质的应用问题；解题的关键是作辅助线，灵活运用平行线的性质、全等三角形的判定及其性质等几何知识点来分析、判断．对综合的分析问题解决问题的能力提出了较高的要求．
练习册系列答案
相关题目
若一次函数y=-2x+b的图象经过（-1，4）
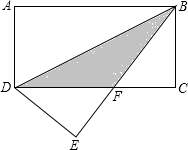如图，将长方形ABCD沿BD对折，点A落在点E处，BE与CD相交于点F，若AD=3，BF=5．
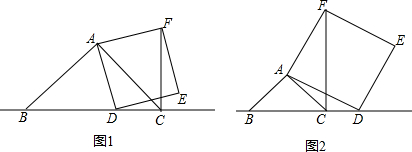
2010年10月26日，沪杭高铁正式通车营运，甲乙两列高速列车在A，B两地之间匀速运行，两车离A地的距离s（千米）随时间t（分）之间的函数关系如图所示，请根据图象回答下列问题：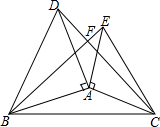
将等腰直角三角尺ABD、ACE如图放置，连接BE、CD．
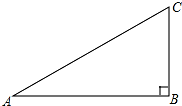如图，在直角三角形ABC中，∠ABC=90°