题目内容
17．
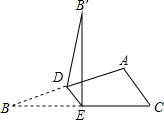如图，在△ABC中，点D、E分别是AB、BC边的中点，∠B=23°，∠C=40°，将△ABC沿DE折叠，点B的对应点是B′，则∠ADB′的度数是（ ）| A． | 45° | B． | 54° | C． | 60° | D． | 65° |
分析 根据三角形的中位线的性质得到DE∥AC，由平行线的性质得到∠BED=∠C=40°，∠EDA=∠B+∠BED=63°，再由折叠的性质得到∠B′=23°，∠DEB′=∠DEB=40°，然后根据三角形的内角和即可得到结果．
解答 解：∵点D、E分别是AB、BC边的中点，
∴DE∥AC，
∴∠BED=∠C=40°，∠EDA=∠B+∠BED=63°，
∵将△ABC沿DE折叠，点B的对应点是B′，
∴∠B′=23°，∠DEB′=∠DEB=40°，
∴∠ADB′=180°-∠B′-∠DEB′-∠ADE=54°，
故选B．
点评 本题考查了折叠问题，三角形的中位线定理，三角形的内角和定理，熟练掌握折叠的性质是解题的关键．
练习册系列答案
相关题目
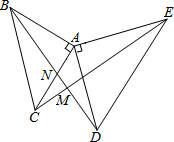如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，CE与BD相交于点M，BD交AC于点N．求证：BD⊥CE．
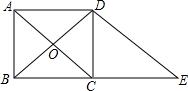如图，在矩形ABCD中，对角线AC、BD相交于点O，过点D作DE∥AC，交BC的延长线于点E．求证：BD=DE．
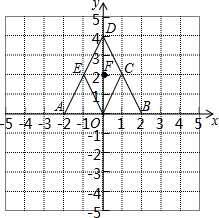如图，指出坐标平面内各点的坐标：A（-2，0），C（1，2），F（0，2）．