题目内容
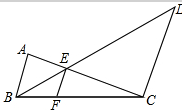如图，AB∥EF∥CD，已知AB=20，CD=80，求EF的长．考点：平行线分线段成比例
专题：
分析：根据平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例，由EF∥AB得到△CEF∽△CAB，则
=
①，同理可得
=
②，则把①与②相加得到
=
+
，然后把AB和CD的长代入计算即可．
| EF |
| AB |
| CF |
| CB |
| EF |
| CD |
| BF |
| BC |
| 1 |
| EF |
| 1 |
| AB |
| 1 |
| CD |
解答：解：∵EF∥AB，
∴△CEF∽△CAB，
∴
=
①，
∵EF∥CD，
∴△BEF∽△BDC，
∴
=
②，
由①+②得
+
=
=1，
∴
=
+
，
即
=
+
，
∴EF=16．
∴△CEF∽△CAB，
∴
| EF |
| AB |
| CF |
| CB |
∵EF∥CD，
∴△BEF∽△BDC，
∴
| EF |
| CD |
| BF |
| BC |
由①+②得
| EF |
| AB |
| EF |
| CD |
| BF+CF |
| BC |
∴
| 1 |
| EF |
| 1 |
| AB |
| 1 |
| CD |
即
| 1 |
| EF |
| 1 |
| 20 |
| 1 |
| 80 |
∴EF=16．
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例；平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．
练习册系列答案
相关题目
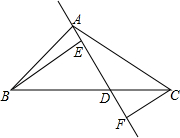在△ABC中，AD是过A的一条射线，交BC于D，过B作BE⊥AD于E，过C作CF⊥AD于F．
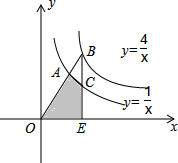如图，过原点的直线交双曲线y=函数y=2-
的最值是（ ）
| -x2+4x |
| A、y最小值=-2，y最大值=2 | ||||
| B、y最小值=1，y最大值=2 | ||||
| C、y最小值=0，y最大值=2 | ||||
D、y最小值=-
|
如图，∠1+∠2=180°，∠A=∠C，求证：AB∥CD．