题目内容
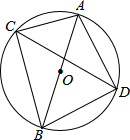 已知A、B、C三点位于⊙O上,其中AB连线过圆心,DC是∠ACB的角平分线,D点也在⊙O上,已知AC=6,AB=10,求BC、AD、BD的长.
已知A、B、C三点位于⊙O上,其中AB连线过圆心,DC是∠ACB的角平分线,D点也在⊙O上,已知AC=6,AB=10,求BC、AD、BD的长.考点:圆周角定理,勾股定理,等腰直角三角形
专题:
分析:由在⊙O中,直径AB的长为10,弦AC=6,利用勾股定理,即可求得BC的长,又由DC是∠ACB的角平分线,可得△ABD是等腰直角三角形,继而求得AD、BD的长.
解答:解:∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵AB=10,AC=6,
∴BC=
=8,
∵DC是∠ACB的角平分线,
∴弧AD=弧BD,
∴AD=BD,
∴∠BAD=∠ABD=45°,
∴AD=BD=
AB=5
.
∴∠ACB=∠ADB=90°,
∵AB=10,AC=6,
∴BC=
| AB2-AC2 |
∵DC是∠ACB的角平分线,
∴弧AD=弧BD,
∴AD=BD,
∴∠BAD=∠ABD=45°,
∴AD=BD=
| ||
| 2 |
| 2 |
点评:此题考查了圆周角定理以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
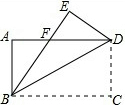 如图,把一张矩形的纸片沿对角线折叠,若BE平分∠ABD,FE=3,CD=3
如图,把一张矩形的纸片沿对角线折叠,若BE平分∠ABD,FE=3,CD=3
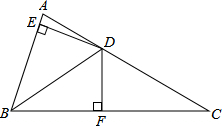 如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,DE⊥AB(E在AB之间),DF⊥BC,已知BD=5,DE=3,CF=4,试求△DFC的周长.
如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,DE⊥AB(E在AB之间),DF⊥BC,已知BD=5,DE=3,CF=4,试求△DFC的周长.