题目内容
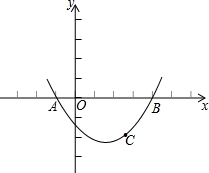 如图,已知抛物线过点A(-1,0),B(4,0),C(
如图,已知抛物线过点A(-1,0),B(4,0),C(| 11 |
| 5 |
| 12 |
| 5 |
(1)求抛物线对应的函数关系式及对称轴;
(2)点C′是点C关于抛物线对称轴的对称点,证明直线y=-
| 4 |
| 3 |
(3)问:以AB为直径的圆能否过点C?并说明理由.
考点:二次函数综合题
专题:
分析:(1)根据待定系数法,可得函数解析式,根据对称轴公式,可得函数图象的对称轴;
(2)根据轴对称的对称点,可得C′点,根据点的坐标满足函数解析式,可得答案;
(3)根据圆心、圆的半径,可得圆的解析式,根据点的坐标是否满足函数解析式,可得答案.
(2)根据轴对称的对称点,可得C′点,根据点的坐标满足函数解析式,可得答案;
(3)根据圆心、圆的半径,可得圆的解析式,根据点的坐标是否满足函数解析式,可得答案.
解答:解:(1)设抛物线的解析式为y=ax2+bx+c,
有函数图象过过点A(-1,0),B(4,0),C(
,-
),得
,
解得
,
抛物线对应的函数关系式是y=
x2-
x-
,
对称轴是x=-
=-
=
;
(2)证明:C′点的坐标是(
,-
),
把C′点的坐标(
,-
)代入y═-
(x+1),得
左边是y=-
,右边=-
(x+1)=-
(
+1)=-
,
左边=右边,
∴直线y=-
(x+1)必经过点C′;
(3)以AB为直径的圆能过点C,理由如下:
以AB为直径的圆是(x-
)2+y2=(
)2,
即(x-
)2+y2=
.
把C点的坐标代入圆的方程的左边,得
(
-
)2+(-
)2=(
-
)2+
=
+
=
,
左边=右边,
C点在以AB为直径的圆上.
有函数图象过过点A(-1,0),B(4,0),C(
| 11 |
| 5 |
| 12 |
| 5 |
|
解得
|
抛物线对应的函数关系式是y=
| 5 |
| 12 |
| 5 |
| 4 |
| 5 |
| 3 |
对称轴是x=-
| b |
| 2a |
-
| ||
2×
|
| 3 |
| 2 |
(2)证明:C′点的坐标是(
| 4 |
| 5 |
| 12 |
| 5 |
把C′点的坐标(
| 4 |
| 5 |
| 12 |
| 5 |
| 4 |
| 3 |
左边是y=-
| 12 |
| 5 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 5 |
| 12 |
| 5 |
左边=右边,
∴直线y=-
| 4 |
| 3 |
(3)以AB为直径的圆能过点C,理由如下:
以AB为直径的圆是(x-
| 3 |
| 2 |
| 5 |
| 2 |
即(x-
| 3 |
| 2 |
| 25 |
| 4 |
把C点的坐标代入圆的方程的左边,得
(
| 11 |
| 5 |
| 3 |
| 2 |
| 12 |
| 5 |
| 22 |
| 10 |
| 15 |
| 10 |
| 144 |
| 25 |
| 49 |
| 100 |
| 576 |
| 100 |
| 25 |
| 4 |
左边=右边,
C点在以AB为直径的圆上.
点评:本题考查了二次函数的综合题,利用了待定系数法求解析式,点的坐标满足函数解析式,点在函数的图象上.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
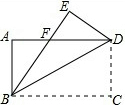 如图,把一张矩形的纸片沿对角线折叠,若BE平分∠ABD,FE=3,CD=3
如图,把一张矩形的纸片沿对角线折叠,若BE平分∠ABD,FE=3,CD=3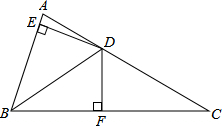 如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,DE⊥AB(E在AB之间),DF⊥BC,已知BD=5,DE=3,CF=4,试求△DFC的周长.
如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,DE⊥AB(E在AB之间),DF⊥BC,已知BD=5,DE=3,CF=4,试求△DFC的周长.