Question

15．已知：如图，QA切⊙O于点A，QB交⊙O于B和C两点，P是$\widehat{BC}$上任意一点，∠P=105°，∠AOC=64°，求∠Q的度数．

Answer 1

分析 连接AC，构建四点共圆，根据圆内接四边形对角互补得：∠BAC=75°，根据圆周角和圆心角的关系求出∠BOC=2∠BAC=150°，利用周角定义求∠AOB的度数，再由等腰三角形的性质和三角形内角和得出结论．

解答 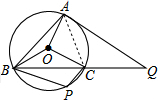解：连接AC，
∵A、B、P、C四点共圆，
∴∠P+∠BAC=180°，
∵∠P=105°，
∴∠BAC=180°-105°=75°，
∴∠BOC=2∠BAC=150°，
∵OB=OC，
∴∠BOC=$\frac{180°-150°}{2}$=15°，
∵∠BOC=150°，∠AOC=64°，
∴∠AOB=360°-150°-64°=146°，
∵OB=OA，
∴∠ABO=∠OAB=17°，
∵QA为⊙O的切线，
在△ABQ中，∴∠Q=180°-17°-15°-17°-90°=41°．

点评 本题考查了切线的性质、四点共圆的性质，同弧所对的圆周角和圆心角的关系、等腰三角形的性质，属于基础题，熟练掌握各性质是关键，依次求出△ABQ其它各角的度数即可．