题目内容
如图，在△ABC中，D为BC边上的一点，| BD |
| DC |
| 1 |
| 2 |
考点：相似三角形的判定与性质
专题：
分析：过B作BE∥AC，交AD延长线于E，易证AE=BE，易证△BED∽△CAD，可得
=
=
，即可求得AE的值，即可求得AC的值，即可解题．
| BD |
| CD |
| ED |
| AD |
| BE |
| AC |
解答：解：过B作BE∥AC，交AD延长线于E，
∵BE∥AC，
∴∠E=∠DAC=120°，
∵∠DAB=30°，
∴∠ABE=30°，
∴AE=BE，
∵BE∥AC，
∴△BED∽△CAD，
∴
=
=
=
，
∵AD=6，
∴DE=3，
∴BE=AE=9，
∴AC=18．
∵BE∥AC，
∴∠E=∠DAC=120°，
∵∠DAB=30°，
∴∠ABE=30°，
∴AE=BE，
∵BE∥AC，
∴△BED∽△CAD，
∴
| BD |
| CD |
| ED |
| AD |
| BE |
| AC |
| 1 |
| 2 |
∵AD=6，
∴DE=3，
∴BE=AE=9，
∴AC=18．
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质，本题中构建并求证△BED∽△CAD是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
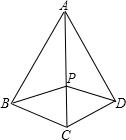如图，在四边形ABCD中，AB=AD，AB⊥BC，AD⊥CD，P是对角线AC上一点，求证：PB=PD．
如图，已知AB∥CD，AB=CD，BF=CE，求证：AE=DF．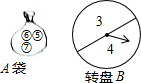
学习概率知识以后，小庆和小丽设计了一个游戏．在一个不透明的布袋A里面装有三个分别标有数字5，6，7的小球（小球除数字不同外，其余都相同）；同时制作了一个可以自由转动的转盘B，转盘B被平均分成2部分，在每一部分内分别标上数字3，4．现在其中一人从布袋A中随机摸取一个小球，记下数字为x；另一人转动转盘B，转盘停止后，指针指向的数字记为y（若指针指在边界线上时视为无效，重新转动），从而确定点P的坐标为P（x，y）．