题目内容
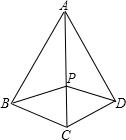 如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥CD,P是对角线AC上一点,求证:PB=PD.
如图,在四边形ABCD中,AB=AD,AB⊥BC,AD⊥CD,P是对角线AC上一点,求证:PB=PD.考点:全等三角形的判定与性质,线段垂直平分线的性质
专题:证明题
分析:易证△ABC和△ADC均为直角三角形,即可证明RT△ABC≌RT△ADC,可得∠BAC=∠DAC,即可证明△BAP≌△DAP,可得PB=PD,即可解题.
解答:证明:∵AB⊥BC,AD⊥CD,
∴△ABC和△ADC均为直角三角形,
在RT△ABC和RT△ADC中,
,
∴RT△ABC≌RT△ADC(HL),
∴∠BAC=∠DAC,
在△BAP和△DAP中,
,
∴△BAP≌△DAP(SAS),
∴PB=PD.
∴△ABC和△ADC均为直角三角形,
在RT△ABC和RT△ADC中,
|
∴RT△ABC≌RT△ADC(HL),
∴∠BAC=∠DAC,
在△BAP和△DAP中,
|
∴△BAP≌△DAP(SAS),
∴PB=PD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证RT△ABC≌RT△ADC和△BAP≌△DAP是解题的关键.

练习册系列答案
相关题目
 如图所示的几何体中,它的主视图是( )
如图所示的几何体中,它的主视图是( )A、 |
B、 |
C、 |
D、 |
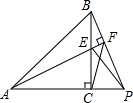 已知△ABC与△ECP为等腰直角三角形,求∠AFC的度数.
已知△ABC与△ECP为等腰直角三角形,求∠AFC的度数.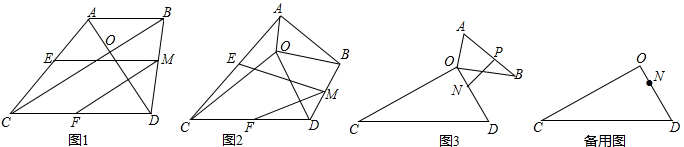
 如图,已知∠C=∠D,∠CAB=∠DBA,AD交BC于点O,请写出图中一组相等的线段
如图,已知∠C=∠D,∠CAB=∠DBA,AD交BC于点O,请写出图中一组相等的线段 如图,在△ABC中,D为BC边上的一点,
如图,在△ABC中,D为BC边上的一点,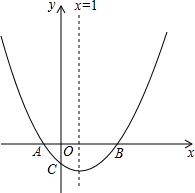 如图,抛物线y=
如图,抛物线y=