题目内容
分解因式：（x+y-z）（x-y+z）+（y-x+z）（y-x-z）
考点：因式分解-提公因式法
专题：
分析：根据提公因式法：提取（x-y+z），再提取2，可分解因式．
解答：解：原式=（x-y+z）[（x+y-z）-（y-x+z）]
=（x-y+z）（x+y-z-y+x-z）
=（x-y+z）（2x-2z）
=2（x-y+z）（x-z）．
=（x-y+z）（x+y-z-y+x-z）
=（x-y+z）（2x-2z）
=2（x-y+z）（x-z）．
点评：本题考查了因式分解，利用了提公因式法分解因式，分解要彻底．
练习册系列答案
相关题目
若x＞-2，则化简|1-|x+3||得（ ）
| A、x+2 | B、-x-2 |
| C、-x-4 | D、x+4 |
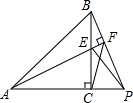已知△ABC与△ECP为等腰直角三角形，求∠AFC的度数．
如图，在△ABC中，D为BC边上的一点，