题目内容
计算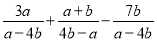 得( )
得( )
A. 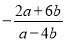 B.
B. 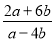 C.
C. 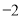 D. 2
D. 2
 D
【解析】试题分析:
=
=
=
=
=2.
故选D.
D
【解析】试题分析:
=
=
=
=
=2.
故选D.
练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
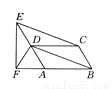
如图所示,在 ABCD中,CE∥BD,EF⊥AB交BA延长线于点F,E,D,A在一条直线上,那么有DF=
ABCD中,CE∥BD,EF⊥AB交BA延长线于点F,E,D,A在一条直线上,那么有DF=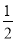 AE,请你说明理由.(提示:直角三角形中斜边中线等于斜边的一半)
AE,请你说明理由.(提示:直角三角形中斜边中线等于斜边的一半)
 答案见解析
【解析】试题分析:首先根据平行四边形的性质可得AD=BC,AD∥BC,再证明四边形EDBC是平行四边形,可得ED=CB,然后根据直角三角形斜边上的中线等于斜边的一半可得结论.
试题解析:证明:∵四边形ABCD为平行四边形,∴AD=BC,AD∥BC.∵CE∥BD,∴四边形EDBC是平行四边形,∴ED=CB,∴ED=AD.∵EF⊥AB,∴△EFA是直角三角形,∴DF=AE.
答案见解析
【解析】试题分析:首先根据平行四边形的性质可得AD=BC,AD∥BC,再证明四边形EDBC是平行四边形,可得ED=CB,然后根据直角三角形斜边上的中线等于斜边的一半可得结论.
试题解析:证明:∵四边形ABCD为平行四边形,∴AD=BC,AD∥BC.∵CE∥BD,∴四边形EDBC是平行四边形,∴ED=CB,∴ED=AD.∵EF⊥AB,∴△EFA是直角三角形,∴DF=AE. 若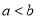 ,则下列各式中一定成立的是( )
,则下列各式中一定成立的是( )
A. 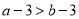 B.
B. 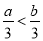 C.
C. 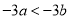 D.
D. 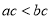
 B
【解析】因为不等式的两边同时加上(或减去)同一个数(或式子),不等号的方向不变,所以A正确;不等式的两边同时乘(或除以)同一个正数,不等号的方向不变,所以B错误;因为2<3,但22<32,所以C错误;当c为负数时,ac>bc,故选A.
B
【解析】因为不等式的两边同时加上(或减去)同一个数(或式子),不等号的方向不变,所以A正确;不等式的两边同时乘(或除以)同一个正数,不等号的方向不变,所以B错误;因为2<3,但22<32,所以C错误;当c为负数时,ac>bc,故选A. 如图,△ABC和△DCE都是边长为2的等边三角形,点B,C,E在同一条直线上,连接BD,则BD的长为( )
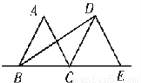
A. 18 B. 3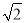 C. 12 D. 2
C. 12 D. 2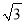
 D
【解析】过点D作DF⊥EC于点F,利用正三角形的性质得出CF=1,BF=3,再利用勾股定理求出DF==,则可得BD=.
故选:D.
D
【解析】过点D作DF⊥EC于点F,利用正三角形的性质得出CF=1,BF=3,再利用勾股定理求出DF==,则可得BD=.
故选:D. 一个直角三角形的两条直角边长分别为6 cm和8 cm,那么这个直角三角形的斜边长为( )
A. 6 cm B. 8 cm C. 10 cm D. 24 cm
 C
【解析】根据勾股定理可以得出:斜边长==10cm.
故选:C.
C
【解析】根据勾股定理可以得出:斜边长==10cm.
故选:C. 若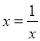 ,则分式
,则分式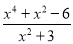 的值为( )
的值为( )
A. 0 B. 1 C. -1 D. -2
 C
【解析】试题分析:∵即x2=1,
==x2-2=1-2=-1,
故选C.
C
【解析】试题分析:∵即x2=1,
==x2-2=1-2=-1,
故选C. 计算: 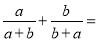 ________.
________.
 1
【解析】试题分析:原式=
=
=1.
故答案为:1.
1
【解析】试题分析:原式=
=
=1.
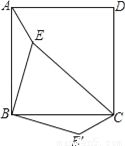
故答案为:1. 如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=__度.
 135
【解析】试题分析:首先根据旋转的性质得出,△EBE′是直角三角形,进而得出∠BEE′=∠BE′E=45°,即可得出答案.
【解析】
连接EE′
∵△ABE绕点B顺时针旋转90°到△CBE′
∴∠EBE′是直角,∴△EBE′是直角三角形,
∵△ABE与△CE′B全等
∴BE=BE′=2,∠AEB=∠BE′C
∴∠BEE′=∠BE′E=45°,
...
135
【解析】试题分析:首先根据旋转的性质得出,△EBE′是直角三角形,进而得出∠BEE′=∠BE′E=45°,即可得出答案.
【解析】
连接EE′
∵△ABE绕点B顺时针旋转90°到△CBE′
∴∠EBE′是直角,∴△EBE′是直角三角形,
∵△ABE与△CE′B全等
∴BE=BE′=2,∠AEB=∠BE′C
∴∠BEE′=∠BE′E=45°,
... 爸爸买彩票,( )中奖.
A. 一定 B. 可能 C. 不可能 D. 以上都不对
 B
【解析】对于买彩票,一定有人中奖,这是一个必然事件;但是对于是谁中奖,这是一个随机事件.所以“爸爸买彩票,中奖”这是一个随机事件.
故选B.
B
【解析】对于买彩票,一定有人中奖,这是一个必然事件;但是对于是谁中奖,这是一个随机事件.所以“爸爸买彩票,中奖”这是一个随机事件.
故选B. 
