题目内容
13.解方程(组)(1)$\frac{2y-1}{3}$=$\frac{y+2}{4}$-1
(2)$\left\{\begin{array}{l}{9s-13t+2=0}\\{s=2-3t}\end{array}\right.$.
分析 (1)按解一元一次方程的步骤进行解方程,注意去分母时-1不能漏乘12;
(2)利用代入法解二元一次方程组.
解答 解:(1)$\frac{2y-1}{3}$=$\frac{y+2}{4}$-1,
去分母得:4(2y-1)=3(y+2)-12,
去括号得:8y-4=3y+6-12,
移项得:8y-3y=-6+4,
合并同类项得:5y=-2,
系数化为1得:y=-$\frac{2}{5}$;
(2)$\left\{\begin{array}{l}{9s-13t+2=0①}\\{s=2-3t②}\end{array}\right.$,
把②代入①得:9(2-3t)-13t+2=0,
18-27t-13t+2=0,
t=$\frac{1}{2}$,
把t=$\frac{1}{2}$代入②得:s=$\frac{1}{2}$,
∴$\left\{\begin{array}{l}{t=\frac{1}{2}}\\{s=\frac{1}{2}}\end{array}\right.$.
点评 本题考查了解二元一次方程组和一元一次方程,注意解二元一次方程组的方法有两种:代入法和加减法;解一元一次方程的步骤为:去分母、去括号、移项、合并同类项、系数化为1,把方程化为形如x=a的形式.

练习册系列答案
相关题目
19.用科学记数法表示0.000043这个数的结果为( )
| A. | 4.3×10-4 | B. | 4.3×10-5 | C. | 4.3×10-6 | D. | 43×10-5 |
2.下列计算正确的是( )
| A. | a6÷a2=a3 | B. | $\sqrt{9}$+$\sqrt{2}$=3$\sqrt{2}$ | C. | (a2)3=a6 | D. | (a+b)2=a2+b2 |


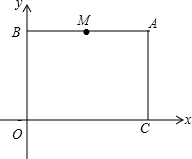 平面直角坐标系中,O是坐标原点,点A是第一象限内一点,A(m,n)满足$\left\{{\begin{array}{l}2m-n=10\\ m-2n=-4\end{array}}\right.$过点A分别作x轴和y轴的平行线,交y轴于点B,交x轴于点C.M是线段AB的中点,点P从M点出发沿线段MA-AC向终点C运动,速度为每秒2个单位长度.设点P运动的时间为t(秒).
平面直角坐标系中,O是坐标原点,点A是第一象限内一点,A(m,n)满足$\left\{{\begin{array}{l}2m-n=10\\ m-2n=-4\end{array}}\right.$过点A分别作x轴和y轴的平行线,交y轴于点B,交x轴于点C.M是线段AB的中点,点P从M点出发沿线段MA-AC向终点C运动,速度为每秒2个单位长度.设点P运动的时间为t(秒).