题目内容
3.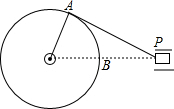 如图是某机械传动装置的静止状态,连杆AP与半径为15cm的转轮相切,此时测得PB=24cm.当该机械传动装置转动时,点P离转轮的最近距离是36cmcm.
如图是某机械传动装置的静止状态,连杆AP与半径为15cm的转轮相切,此时测得PB=24cm.当该机械传动装置转动时,点P离转轮的最近距离是36cmcm.
分析 设圆心为O,当PA与⊙O相切时,点P离转轮的距离最近,即切线长AP,根据勾股定理求得AP=$\sqrt{O{P}^{2}-O{A}^{2}}$=36cm,即可得到点P离转轮的最近距离是36cm.
解答  解:设圆心为O,当PA与⊙O相切时,点P离转轮的距离最近,
解:设圆心为O,当PA与⊙O相切时,点P离转轮的距离最近,
即切线长AP,
∵∠OAP=90°,OA=15,OP=24+15,
∴AP=$\sqrt{O{P}^{2}-O{A}^{2}}$=36cm,
∴点P离转轮的最近距离是36cm.
故答案为:36cm.
点评 本题考查了切线的性质,勾股定理,熟练掌握切线的性质是解题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
18.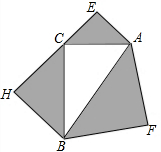 如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
 如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )| A. | 130 | B. | 120 | C. | 100 | D. | 90 |
5.对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间存在一次函数关系.从温度计的刻度上可以看出,摄氏温度x(℃)与华氏温度y(℉)有如下的对应关系:
(1)试确定y与x之间的函数关系式;
(2)某天,南昌的最高气温是25℃,澳大利亚悉尼的最高气温80℉,这一天哪个地区的最高气温较高?
| x(℃) | … | -10 | 0 | 10 | 20 | 30 | … |
| y(℉) | … | 14 | 32 | 50 | 68 | 86 | … |
(2)某天,南昌的最高气温是25℃,澳大利亚悉尼的最高气温80℉,这一天哪个地区的最高气温较高?
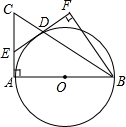 如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AC于点E,BF⊥DE于点F.
如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AC于点E,BF⊥DE于点F.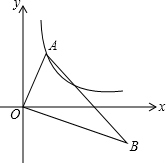 如图,在Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°.若点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上运动,点B在反比例函数y=$\frac{k}{x}$(x>O)的图象上运动,则k=-6.
如图,在Rt△AOB中,O为坐标原点,∠AOB=90°,∠B=30°.若点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上运动,点B在反比例函数y=$\frac{k}{x}$(x>O)的图象上运动,则k=-6. 已知平行四边形ABCD中,AB=BD=CD,且DB⊥AB,求tan∠CAB、tan∠DAC的值.
已知平行四边形ABCD中,AB=BD=CD,且DB⊥AB,求tan∠CAB、tan∠DAC的值.