题目内容
5.对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间存在一次函数关系.从温度计的刻度上可以看出,摄氏温度x(℃)与华氏温度y(℉)有如下的对应关系:| x(℃) | … | -10 | 0 | 10 | 20 | 30 | … |
| y(℉) | … | 14 | 32 | 50 | 68 | 86 | … |
(2)某天,南昌的最高气温是25℃,澳大利亚悉尼的最高气温80℉,这一天哪个地区的最高气温较高?
分析 (1)根据题意可知摄氏温度与华氏温度之间存在一次函数关系,从而可以设出一次函数的解析式,根据表格中的数据可以求出一次函数的解析式;
(2)将x=25代入第一问中求得的函数解析式,可以将南昌的温度转化为华氏温度,从而可以和悉尼的最高气温进行比较,进而得到本题的答案.
解答 解:(1)设摄氏温度与华氏温度之间的一次函数关系是y=kx+b,
∵由表格可得,x=0时,y=32;x=10时,y=50.
∴$\left\{\begin{array}{l}{b=32}\\{10k+b=50}\end{array}\right.$.
解得,k=1.8,b=32.
∴y与x之间的函数关系式是:y=1.8x+32.
即y与x之间的函数关系式时:y=1.8x+32.
(2)将x=25代入y=1.8x+32得,y=1.8×25+32=45+32=77.
∵77<80,
∴悉尼的最高气温较高.
答:这一天澳大利亚悉尼的最高气温较高.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
15.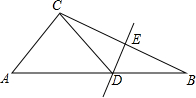 如图,在△ABC中,AC=5,BC=8,BC的中垂线交AB、BC于D、E,DE=3,连CD,当∠ACD=90°时,则AD的长是( )
如图,在△ABC中,AC=5,BC=8,BC的中垂线交AB、BC于D、E,DE=3,连CD,当∠ACD=90°时,则AD的长是( )
 如图,在△ABC中,AC=5,BC=8,BC的中垂线交AB、BC于D、E,DE=3,连CD,当∠ACD=90°时,则AD的长是( )
如图,在△ABC中,AC=5,BC=8,BC的中垂线交AB、BC于D、E,DE=3,连CD,当∠ACD=90°时,则AD的长是( )| A. | 6 | B. | 5$\sqrt{3}$ | C. | 5$\sqrt{2}$ | D. | 8 |
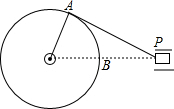 如图是某机械传动装置的静止状态,连杆AP与半径为15cm的转轮相切,此时测得PB=24cm.当该机械传动装置转动时,点P离转轮的最近距离是36cmcm.
如图是某机械传动装置的静止状态,连杆AP与半径为15cm的转轮相切,此时测得PB=24cm.当该机械传动装置转动时,点P离转轮的最近距离是36cmcm.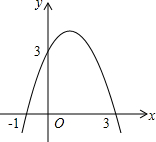 二次函数y=-x2+2x+3的图象如图所示,在x轴上方,且平行于x轴的直线与该二次函数的图象交于M,N两点,在x轴上取点Q,使△MNQ为等腰直角三角形,请你写出所有符合的点Q的坐标(1,0)或(2-$\sqrt{5}$,0)或($\sqrt{5}$,0).
二次函数y=-x2+2x+3的图象如图所示,在x轴上方,且平行于x轴的直线与该二次函数的图象交于M,N两点,在x轴上取点Q,使△MNQ为等腰直角三角形,请你写出所有符合的点Q的坐标(1,0)或(2-$\sqrt{5}$,0)或($\sqrt{5}$,0).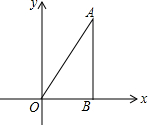 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B旋转60°得到△CBD,若点B的坐标为(2,0),则点A的对应点C的坐标为(-1,$\sqrt{3}$)或(5,$\sqrt{3}$).
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B旋转60°得到△CBD,若点B的坐标为(2,0),则点A的对应点C的坐标为(-1,$\sqrt{3}$)或(5,$\sqrt{3}$).