题目内容
5.在矩形ABCD中,AB=4,BC=5,点E,F,G,H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF,若设AE=a,AF=b,则a与b满足的关系为a+b=3.分析 由题意得出:△BGF∽△AFE,△AEF≌△CGH,再由GF=2EF,得出BG=2b,BF=2a,CG=a,由此根据AB=4,BC=5,列出方程组即可.
解答 解:如图所示;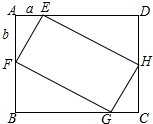
∵四边形ABCD和四边形EFGH是矩形,
∴∠A=∠B=∠C=90°,∠EFG=∠FGH=90°,EF=GH,
∴∠1+2=90°,∠1+∠3=90°,
∴∠2=∠3,
同理∠3=∠5,∴∠2=∠5,
∴△BGF∽△AFE,
∴$\frac{BG}{AF}=\frac{FG}{EF}$=$\frac{BF}{AE}$,
∵GF=2EF,
∴$\frac{BG}{AF}$=$\frac{BF}{AE}$=2,
∴BG=2b,BF=2a,
在△AEF和△CGH中,$\left\{\begin{array}{l}{∠A=∠C}&{\;}\\{∠2=∠5}&{\;}\\{EF=GH}&{\;}\end{array}\right.$,
∴△AEF≌△CGH(AAS),
∴CG=AE=a,
∵AB=4,BC=5,
∴$\left\{\begin{array}{l}{2a+b=4}\\{a+2b=5}\end{array}\right.$,
得:a+b=3;
故答案为:a+b=3.
点评 本题考查了矩形的性质、全等三角形的判定与性质、相似三角形的判定与性质;正确利用矩形的性质,三角形相似、全等的判定与性质从问题中抽象出二元一次方程组是解决问题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
3.多项式a4-3a3+9a+2与多项式3a3-a4+8-4a的和一定是( )
| A. | 偶数 | B. | 奇数 | C. | 10的倍数 | D. | 以上答案郡不对 |
10.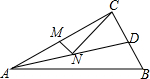 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )
 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{12}{5}$ |
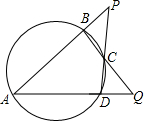 如图,点A、B、C,D在同一圆上,AD,BC延长线相交于点Q,AB,DC的延长线相交于点P.若∠A=50°,∠P=35°,则∠Q=45°.
如图,点A、B、C,D在同一圆上,AD,BC延长线相交于点Q,AB,DC的延长线相交于点P.若∠A=50°,∠P=35°,则∠Q=45°. 如图,在△ABC中,∠A=70°,∠ABC=60°,CD平分∠ACB,BE为AC边上的高,求∠BOC的度数.
如图,在△ABC中,∠A=70°,∠ABC=60°,CD平分∠ACB,BE为AC边上的高,求∠BOC的度数. 如图是一个三角形数阵,根据该数阵的规律,猜想第八行所有数的和是512.
如图是一个三角形数阵,根据该数阵的规律,猜想第八行所有数的和是512.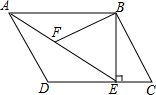 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.