题目内容
13.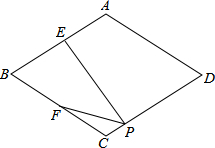 如图,在菱形ABCD中,E、F分别是AB、BC边的中点,EP⊥CD于点P,∠BAD=110°,则∠FPC的度数是55°.
如图,在菱形ABCD中,E、F分别是AB、BC边的中点,EP⊥CD于点P,∠BAD=110°,则∠FPC的度数是55°.
分析 延长PF、EB交于点G;连接EF,易证△BGF≌△CPF,则点F为PG的中点,FP=FG=FE,则∠FPC=∠FGB=∠GEF;连接AC,则∠GEF=∠BAC=$\frac{1}{2}$∠BAD=55°,进而可求出∠FPC的度数.
解答 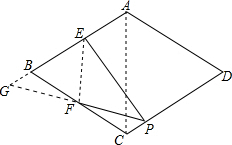 解:延长PF、EB交于点G;连接EF,
解:延长PF、EB交于点G;连接EF,
∵四边形ABCD是菱形,
∴AG∥DC,
∴∠GBF=∠PCF,
∵F是BC中点,
∴BF=CF,
在△BGF和△CPF中,
$\left\{\begin{array}{l}{∠GBF=∠PCF}\\{BF=CF}\\{∠BFG=∠CFP}\end{array}\right.$,
∴△BGF≌△CPF,
∴PF=GF,
∴点F为PG的中点,
∵∠GEP=90°,
∴FP=FG=FE,
∴∠FPC=∠FGB=∠GEF,
连接AC,
则∠GEF=∠BAC=$\frac{1}{2}$∠BAD=55°,
∴∠FPC的度数是55°,
故答案为:55°.
点评 本题考查了菱形的性质、全等三角形的判定和性质、直角三角形斜边上的中线的性质,题目的综合性较强难度较大,解题的关键是正确添加辅助线,构造全等三角形,从而得到点F为PG的中点.

练习册系列答案
相关题目
3.2015年,永州市政府工作报告指出,要大力发展现代农业,做强优势产业,确保粮食面积825万亩,水果150万亩,蔬菜230万亩,烤烟25万亩.其中粮食面积825万亩中的“825万”用科学记数法表示为( )
| A. | 8.25×107 | B. | 8.25×106 | C. | 82.5×105 | D. | 0.825×107 |
5.在平面直角坐标系中,若点P(m,1)在第二象限,则点Q(-m,0)在( )
| A. | x轴正半轴上 | B. | y轴正半轴上 | C. | x轴负半轴上 | D. | y轴负半轴上 |

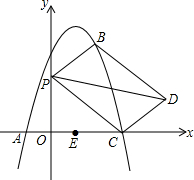 如图,抛物线y=ax2+bx+c经过点A(-1,0),E(0,5),B(2,5)三点,抛物线与x轴的另一个交点为C点,点P为y轴上一动点,作平行四边形BPCD.
如图,抛物线y=ax2+bx+c经过点A(-1,0),E(0,5),B(2,5)三点,抛物线与x轴的另一个交点为C点,点P为y轴上一动点,作平行四边形BPCD. 如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE. 如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=35°,则∠2=125°.
如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=35°,则∠2=125°.