题目内容
1．在方程组$\left\{\begin{array}{l}{2x+y=2-\frac{m}{3}}\\{x+2y=1}\end{array}\right.$中，若未知数x、y满足x-y＞-6．求m的取值范围．分析 将两二元一次方程组相减，进而得出x-y=1-$\frac{m}{3}$，求出即可．
解答 解：由题意可得：2x+y-（x+2y）=x-y=2-$\frac{m}{3}$-1=1-$\frac{m}{3}$＞-6，
则m＜21．
点评 此题主要考查了二元一次方程组的解，正确将已知变形求出是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
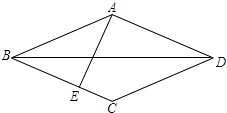已知：如图，在菱形ABCD中，AE⊥BC，垂足为E，对角线BD=4，tan∠CBD=$\frac{1}{2}$，则AB=$\sqrt{5}$，sin∠ABE=$\frac{4}{5}$．
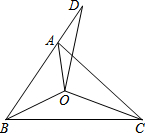如图，已知△ABC三个内角的平分线交于点O，延长BA到点D，使AD=AO，连接DO，若BD=BC，∠ABC=54°，则∠BCA的度数为42°．
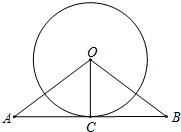如图，在等腰△OAB中，OA=OB，以点O为圆心，作圆与底边AB相切于点C．
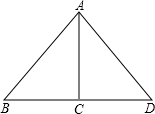我们把两个三角形的外心之间的距离叫做外心距．如图，在Rt△ABC和Rt△ACD中，∠ACB=∠ACD=90°，点D在边BC的延长线上，如果BC=DC=3，那么△ABC和△ACD的外心距是3．
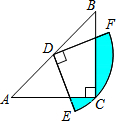如图，在△ABC中，CA=CB，∠ACB=90°，AB=2，点D为AB的中点，以点D为圆心作圆心角为90°的扇形DEF，点C恰在弧EF上，则图中阴影部分的面积为$\frac{π}{4}$-$\frac{1}{2}$．
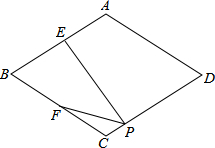如图，在菱形ABCD中，E、F分别是AB、BC边的中点，EP⊥CD于点P，∠BAD=110°，则∠FPC的度数是55°．