题目内容
16.若直角三角形的两条直角边长分别是6和8,则它的外接圆半径为( )| A. | $\sqrt{7}$ | B. | 4 | C. | 5 | D. | 10 |
分析 首先根据勾股定理,得斜边是10,再根据其外接圆的半径是斜边的一半,得出其外接圆的半径.
解答 解:∵直角边长分别为6和8,
∴斜边=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴这个直角三角形的外接圆的半径=$\frac{1}{2}$×10=5.
故选C.
点评 本题考查的是直角三角形的外接圆半径,重点在于理解直角三角形的外接圆是以斜边中点为圆心,斜边长的一半为半径的圆.

练习册系列答案
相关题目
11.同时含有字母a,b,c,系数为1的6次单项式按以下规则排序:先看a的次数,a的次数高的单项式排在前面,若相同,再比较b的次数,最后比较c的次数,均是先高次后低次,则a2b3c排在第几位( )
| A. | 第4位 | B. | 第5位 | C. | 第6位 | D. | 第7位 |
1.已知甲数比乙数的2倍少1,设甲数为x,则乙数可表示为( )
| A. | 2x-1 | B. | 2x+1 | C. | $\frac{1}{2}({x-1})$ | D. | $\frac{1}{2}({x+1})$ |
 如图,?ABCD中,AB>BC,∠BAD与∠ADC的平分线交于点E,∠ABC与∠BCD的平分线交于点F.
如图,?ABCD中,AB>BC,∠BAD与∠ADC的平分线交于点E,∠ABC与∠BCD的平分线交于点F.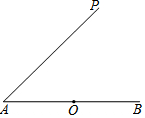 如图,已知O是∠PAB的一边AB上的点,按要求作图:
如图,已知O是∠PAB的一边AB上的点,按要求作图: 如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为30米的篱笆围成,若墙长为18米,设这个苗圃垂直于墙的一边长为x米.
如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为30米的篱笆围成,若墙长为18米,设这个苗圃垂直于墙的一边长为x米. 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置,如果BC=2,那么线段BE的长度为$\sqrt{2}$.
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置,如果BC=2,那么线段BE的长度为$\sqrt{2}$. 如图,在△ABC中,∠ACB=90°,AC=BC=4,D为BC的中点,DE⊥AB,垂足为E.过点B作BF∥AC交DE的延长线于点F,连接CF,AF.现有如下结论:
如图,在△ABC中,∠ACB=90°,AC=BC=4,D为BC的中点,DE⊥AB,垂足为E.过点B作BF∥AC交DE的延长线于点F,连接CF,AF.现有如下结论: