题目内容
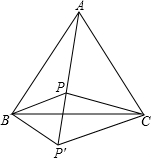 P为等边△ABC内的一点,PA=5,PB=3,PC=4,将△ABP绕点B顺时针旋转到△CBP′位置.
P为等边△ABC内的一点,PA=5,PB=3,PC=4,将△ABP绕点B顺时针旋转到△CBP′位置.①判断△BPP′的形状,并说明理由;
②求∠BPC的度数.
考点:旋转的性质,等边三角形的判定与性质,勾股定理的逆定理
专题:
分析:①根据旋转的性质可得BP=BP′,∠PBP′=∠ABC=60°,然后根据有一个角是60°的等腰三角形是等边三角形解答即可;
②根据等边三角形的三条边都相等可得PP′=PB,三个角都是60°可得∠BPP′=60°,根据旋转的性质可得P′C=PA,然后利用勾股定理逆定理判断出∠CPP′=90°,然后根据∠BPC=∠BPP′+∠CPP′计算即可得解.
②根据等边三角形的三条边都相等可得PP′=PB,三个角都是60°可得∠BPP′=60°,根据旋转的性质可得P′C=PA,然后利用勾股定理逆定理判断出∠CPP′=90°,然后根据∠BPC=∠BPP′+∠CPP′计算即可得解.
解答:解:①∵△ABC是等边三角形,
∴∠ABC=60°,
∵△ABP绕点B顺时针旋转得到△CBP′,
∴BP=BP′,∠PBP′=∠ABC=60°,
∴△BPP′是等边三角形;
②∵△BPP′是等边三角形,
∴PP′=PB,∠BPP′=60°,
由旋转的性质得,P′C=PA=5,
∵PP′2+PC2=32+42=25=P′C2,
∴△CPP′是直角三角形,∠CPP′=90°,
∴∠BPC=∠BPP′+∠CPP′=60°+90°=150°.
∴∠ABC=60°,
∵△ABP绕点B顺时针旋转得到△CBP′,
∴BP=BP′,∠PBP′=∠ABC=60°,
∴△BPP′是等边三角形;
②∵△BPP′是等边三角形,
∴PP′=PB,∠BPP′=60°,
由旋转的性质得,P′C=PA=5,
∵PP′2+PC2=32+42=25=P′C2,
∴△CPP′是直角三角形,∠CPP′=90°,
∴∠BPC=∠BPP′+∠CPP′=60°+90°=150°.
点评:本题考查了旋转的性质,等边三角形的判定与性质,勾股定理逆定理,熟记性质与等边三角形的判断方法是解题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图,△ABC的中线BE、CF相交于点G,则GE:GB=( )
如图,△ABC的中线BE、CF相交于点G,则GE:GB=( )| A、1:2 | B、1:3 |
| C、2:3 | D、2:5 |
 如图,直线l与⊙O相切于A,弦BC交半径OA于D,GB⊥BC交l于G,若OA=R,AD=a,AC=b,则DG=
如图,直线l与⊙O相切于A,弦BC交半径OA于D,GB⊥BC交l于G,若OA=R,AD=a,AC=b,则DG= 如图,由单位正方形拼成的“工“字形中,顶点为小正方形顶点的等腰直角三角形有
如图,由单位正方形拼成的“工“字形中,顶点为小正方形顶点的等腰直角三角形有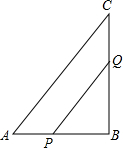 如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始,沿AB边向点B以每秒1cm的速度移动,点Q从点B开始,沿着BC边向点C以每秒2cm的速度移动,如果P、Q同时出发,问:经过几秒钟△PBQ的面积最大?最大面积是多少?
如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始,沿AB边向点B以每秒1cm的速度移动,点Q从点B开始,沿着BC边向点C以每秒2cm的速度移动,如果P、Q同时出发,问:经过几秒钟△PBQ的面积最大?最大面积是多少?