题目内容
 如图,直线l与⊙O相切于A,弦BC交半径OA于D,GB⊥BC交l于G,若OA=R,AD=a,AC=b,则DG=
如图,直线l与⊙O相切于A,弦BC交半径OA于D,GB⊥BC交l于G,若OA=R,AD=a,AC=b,则DG=考点:切线的性质
专题:计算题
分析:作直径AE,连结CE、AB,如图,根据切线的性质,由直线l与⊙O相切于A得到∠DAG=90°,而GB⊥BC,则∠DBG=90°,根据圆周角定理可得点B和点A在以DG为直径的圆上,即点B、D、A、G四点共圆,所以∠DAA=∠DGA,加上∠CBA=∠E,则∠DGA=∠E,然后证明Rt△DAG∽Rt△ACE,再利用相似比可计算出DG.
解答: 解:作直径AE,连结CE、AB,如图,
解:作直径AE,连结CE、AB,如图,
∵直线l与⊙O相切于A,
∴OA⊥AG,
∴∠DAG=90°,
∵GB⊥BC,
∴∠DBG=90°,
∴点B和点A在以DG为直径的圆上,即点B、D、A、G四点共圆,
∴∠DBA=∠DGA,
∵∠CBA=∠E,
∴∠DGA=∠E,
∵AE为直径,
∴∠ACE=90°,
∴Rt△DAG∽Rt△ACE,
∴
=
,即
=
,
∴DG=
.
故答案为
.
 解:作直径AE,连结CE、AB,如图,
解:作直径AE,连结CE、AB,如图,∵直线l与⊙O相切于A,
∴OA⊥AG,
∴∠DAG=90°,
∵GB⊥BC,
∴∠DBG=90°,
∴点B和点A在以DG为直径的圆上,即点B、D、A、G四点共圆,
∴∠DBA=∠DGA,
∵∠CBA=∠E,
∴∠DGA=∠E,
∵AE为直径,
∴∠ACE=90°,
∴Rt△DAG∽Rt△ACE,
∴
| DG |
| AE |
| DA |
| AC |
| DG |
| 2R |
| a |
| b |
∴DG=
| 2Ra |
| b |
故答案为
| 2Ra |
| b |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理和相似三角形的判定与性质.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图,某学校要在校园内墙边的空地上修建一个长方形的存车处,存车处的两面靠墙(一面墙AB长40m,另一面墙AC长50米.),另外两面用80m长的铁栅栏围起来,如果这个存车处的面积为1575m2,求这个长方形存车处借助墙AB的长.
如图,某学校要在校园内墙边的空地上修建一个长方形的存车处,存车处的两面靠墙(一面墙AB长40m,另一面墙AC长50米.),另外两面用80m长的铁栅栏围起来,如果这个存车处的面积为1575m2,求这个长方形存车处借助墙AB的长.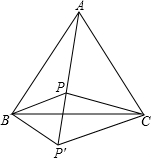 P为等边△ABC内的一点,PA=5,PB=3,PC=4,将△ABP绕点B顺时针旋转到△CBP′位置.
P为等边△ABC内的一点,PA=5,PB=3,PC=4,将△ABP绕点B顺时针旋转到△CBP′位置.