题目内容
9. 如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y轴上,S?ABCD=4,则下列点在反比例函数y=$\frac{k}{x}$(x<0)图象上的是( )
如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y轴上,S?ABCD=4,则下列点在反比例函数y=$\frac{k}{x}$(x<0)图象上的是( )| A. | (-2,4) | B. | (-4,1) | C. | (-3,2) | D. | (-2,1) |
分析 作AE⊥BC于E,由四边形ABCD为平行四边形得AD∥x轴,则可判断四边形ADOE为矩形,所以S平行四边形ABCD=S矩形ADOE,根据反比例函数k的几何意义得到S矩形ADOE=|-k|=4,从而得出k=-4,因为B点的横坐标和纵坐标的积等于-4,即可判断(-4,1)在反比例函数的图象上.
解答 解: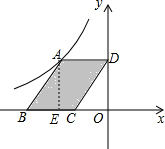 作AE⊥BC于E,如图,
作AE⊥BC于E,如图,
∵四边形ABCD为平行四边形,
∴AD∥x轴,
∴四边形ADOE为矩形,
∴S平行四边形ABCD=S矩形ADOE,
而S矩形ADOE=|-k|,
∴|-k|=4,
而k<0,
∴k=-4.
∵-4×1=-4,
∴点(-4,1)是反比例函数图象上的点,
故选B.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列四张扑克牌中,属于中心对称的图形是( )
| A. |  红桃7 | B. |  方块4 | C. |  梅花6 | D. |  黑桃5 |
4.下列几何体的主视图、左视图、俯视图都相同的是( )
| A. |  | B. |  | C. |  | D. |  |
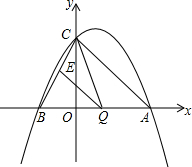 如图,已知抛物线与y轴交于点C(0,4),与x轴交于A(x1,0)、B(x2,0),其中x1,x2为方程x2-2x-8=0的两个根.
如图,已知抛物线与y轴交于点C(0,4),与x轴交于A(x1,0)、B(x2,0),其中x1,x2为方程x2-2x-8=0的两个根.