题目内容
17.求不等式组$\left\{\begin{array}{l}{\frac{x+2}{3}<1}\\{2(1-x)≤5}\end{array}\right.$的整数解.分析 首先得出一元一次不等式组中x的取值,根据x是整数解得出x的可能取值.
解答 解:$\left\{\begin{array}{l}{\frac{x+2}{3}<1}\\{2(1-x)≤5}\end{array}\right.$,
解不等式①得x<1,
解不等式②得x≥-$\frac{3}{2}$,不等式组的解集为-$\frac{3}{2}$≤x<1,
因此不等式组的整数解是-1,0.
点评 此题考查的是一元一次不等式的解法和一元一次方程的解,根据x的取值范围,得出x的整数解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
5.不为0的四个实数a、b,c、d满足ab=cd,改写成比例式错误的是( )
| A. | $\frac{a}{c}$=$\frac{d}{b}$ | B. | $\frac{c}{a}$=$\frac{b}{d}$ | C. | $\frac{d}{a}$=$\frac{b}{c}$ | D. | $\frac{a}{b}$=$\frac{c}{d}$ |
9. 如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y轴上,S?ABCD=4,则下列点在反比例函数y=$\frac{k}{x}$(x<0)图象上的是( )
如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y轴上,S?ABCD=4,则下列点在反比例函数y=$\frac{k}{x}$(x<0)图象上的是( )
 如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y轴上,S?ABCD=4,则下列点在反比例函数y=$\frac{k}{x}$(x<0)图象上的是( )
如图,点A是反比例函数y=$\frac{k}{x}$(x<0)图象上的一点,过点A作平行四边形ABCD,使点B,C在x轴上,点D在y轴上,S?ABCD=4,则下列点在反比例函数y=$\frac{k}{x}$(x<0)图象上的是( )| A. | (-2,4) | B. | (-4,1) | C. | (-3,2) | D. | (-2,1) |
7.测定某运动员跑100m的平均速度,测的结果是跑完前24m用了3s,跑完后76m又用了6s,该运动员的平均速度是( )
| A. | 8m/s | B. | 11.1m/s | C. | 12.7m/s | D. | 10.35m/s |
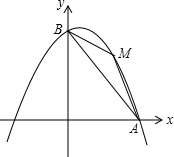 如图,抛物线y=a(x-1)2+b经过A(4,0)和B(0,4)两点.
如图,抛物线y=a(x-1)2+b经过A(4,0)和B(0,4)两点.