题目内容
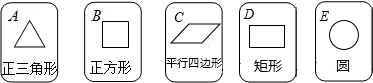
14．如图，有5张背面相同的纸牌A，B，C，D，E，其正面分别画有五个不同的几何图形，将这5张纸牌背面朝上洗匀后，小明随机摸出一张，记下图形后放回洗匀，小亮随机再摸出一张．（1）用列表法（或树状图）求解表示两次摸牌的所有可能结果（纸牌用A，B，C，D，E表示）；
（2）小明和小亮约定做一个游戏，其规则为：若摸出两张牌面图形都是轴对称图形小明赢，若摸出两张牌面图形都是中心对称图形小亮赢，这个游戏公平吗？请说明理由．
分析 （1）首先根据题意画出树状图，然后由树状图求得所有等可能的结果；
（2）首先根据（1）求得摸出两张牌面图形都是轴对称图形的有16种情况，若摸出两张牌面图形都是中心对称图形的有16种情况，继而求得小明赢与小亮赢的概率，比较概率的大小，即可知这个游戏是否公平．
解答 解：（1）画树状图得：
则共有25种等可能的结果；
（2）这个游戏公平．
∵摸出两张牌面图形都是轴对称图形的有16种情况，若摸出两张牌面图形都是中心对称图形的有16种情况，
∴P（小明赢）=P（小亮赢）=$\frac{16}{25}$，
∴这个游戏公平．
点评 本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．
练习册系列答案
相关题目
如图，平行四边形ABCD的顶点A，B，D的坐标分别是（0，0）、（5，0）、（2，3），则顶点C的坐标是（7，3）．
5．不为0的四个实数a、b，c、d满足ab=cd，改写成比例式错误的是（ ）
| A． | $\frac{a}{c}$=$\frac{d}{b}$ | B． | $\frac{c}{a}$=$\frac{b}{d}$ | C． | $\frac{d}{a}$=$\frac{b}{c}$ | D． | $\frac{a}{b}$=$\frac{c}{d}$ |
9．
如图，点A是反比例函数y=$\frac{k}{x}$（x＜0）图象上的一点，过点A作平行四边形ABCD，使点B，C在x轴上，点D在y轴上，S?ABCD=4，则下列点在反比例函数y=$\frac{k}{x}$（x＜0）图象上的是（ ）
如图，点A是反比例函数y=$\frac{k}{x}$（x＜0）图象上的一点，过点A作平行四边形ABCD，使点B，C在x轴上，点D在y轴上，S?ABCD=4，则下列点在反比例函数y=$\frac{k}{x}$（x＜0）图象上的是（ ）| A． | （-2，4） | B． | （-4，1） | C． | （-3，2） | D． | （-2，1） |