题目内容
19．七年级（1）班买了若干本4元及7元的笔记本作为奖品，共花费40元，则这两种笔记本的数量可能相差（ ）| A． | 1 | B． | 4 | C． | 1或4 | D． | 不确定 |
分析 设购买4元笔记本x本，7元笔记本y本，根据总价=单价×数量，即可得出关于x、y的二元一次方程，由x、y均为正整数即可得出x、y的值，二者做差后即可得出结论．
解答 解：设购买4元笔记本x本，7元笔记本y本，
根据题意得：4x+7y=40，
∴x=10-$\frac{7}{4}$y．
∵x、y均为正整数，
∴当y=4时，x=3．
∴y-x=4-3=1．
故选A．
点评 本题考查了二元一次方程的应用，根据总价=单价×数量列出关于x、y的二元一次方程是解题的关键．
练习册系列答案
相关题目
9．下列哪个点在函数y=3-2x的图象上（ ）
| A． | （3，-2） | B． | （0，$\frac{3}{2}$） | C． | （3，0） | D． | （$\frac{3}{2}$，0） |
7．如果a表示不为0的任意一个实数，那么下列四个算式中，正确的是（ ）
| A． | 3a3-2a2=0 | B． | a3•a${\;}^{\frac{1}{3}}$=a | C． | a3÷a2=a | D． | （a2）${\;}^{\frac{1}{2}}$=a${\;}^{\frac{5}{2}}$ |
14．
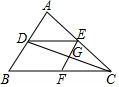如图，DE∥BC，EF∥AB，则下列结论错误的是（ ）
如图，DE∥BC，EF∥AB，则下列结论错误的是（ ）| A． | $\frac{EG}{AD}$=$\frac{CE}{CA}$ | B． | $\frac{EC}{EA}$=$\frac{CF}{BF}$ | C． | $\frac{DG}{GC}$=$\frac{DE}{FC}$ | D． | $\frac{CG}{DG}$=$\frac{CF}{AE}$ |
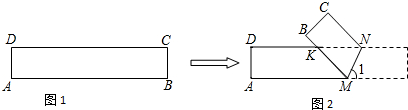
8．
如图，等边三角形纸片ABC中，AB=4．D是AB边的中点，E是BC边上一点现将△BDE沿DE折叠，得△B'DE．连接CB'，则CB'长度的最小值为（ ）
如图，等边三角形纸片ABC中，AB=4．D是AB边的中点，E是BC边上一点现将△BDE沿DE折叠，得△B'DE．连接CB'，则CB'长度的最小值为（ ）| A． | 2$\sqrt{3}$-2 | B． | 1 | C． | $\sqrt{3}$-1 | D． | 2 |
9．
如图，OA⊥OB，等腰直角三角形CDE的腰CD在OB上，∠ECD=45°，将三角形CDE绕点C逆时针旋转75°，点E的对应点N恰好落在OA上，则$\frac{OC}{CD}$的值为（ ）
如图，OA⊥OB，等腰直角三角形CDE的腰CD在OB上，∠ECD=45°，将三角形CDE绕点C逆时针旋转75°，点E的对应点N恰好落在OA上，则$\frac{OC}{CD}$的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{2}}}{2}$ |