题目内容
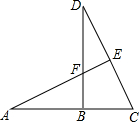 如图,已知BD⊥AC,AE⊥CD,BF=BC,求证:AF=CD.
如图,已知BD⊥AC,AE⊥CD,BF=BC,求证:AF=CD.考点:全等三角形的判定与性质
专题:证明题
分析:由条件可得出∠A=∠D,再结合BF=BC,AAS证明△ABF≌△DBC,可得结论.
解答:证明:∵BD⊥AC,AE⊥CD,
∴∠A+∠C=∠D+∠C=90°,
∴∠A=∠D,
在△ABF和△DBC中,
,
∴△ABF≌△DBC(AAS),
∴AF=CD.
∴∠A+∠C=∠D+∠C=90°,
∴∠A=∠D,
在△ABF和△DBC中,
|
∴△ABF≌△DBC(AAS),
∴AF=CD.
点评:本题主要考查三角形全等的判定和性质,找出∠A=∠D是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
A、B两城相距720km,普快列车从A城出发120km后,特快列车从B城开往A城,6h后两车相遇.若普快列车是特快列车速度的
,且设普快列车速度为xkm/h,则下列所列方程错误的是( )
| 2 |
| 3 |
A、720-6x=6×
| ||
B、720+120=6(x+
| ||
C、6x+6×
| ||
D、6(x+
|
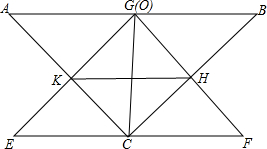 如图所示,在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,现将一个三角板EGF的直角顶点G放在点O处,把△EFG绕点O旋转,EG交直线AC于点K,FG交直线BC于点H.
如图所示,在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,现将一个三角板EGF的直角顶点G放在点O处,把△EFG绕点O旋转,EG交直线AC于点K,FG交直线BC于点H. 有理数a、b在数轴上的位置如图所示:化简|a-b|-(-a)-|b|=
有理数a、b在数轴上的位置如图所示:化简|a-b|-(-a)-|b|=