题目内容
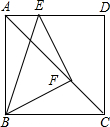 如图,已知正方形ABCD,在AD、AC上分别取E、F两点,使ED:AD=2FC:AC,求证:△BEF是等腰直角三角形.
如图,已知正方形ABCD,在AD、AC上分别取E、F两点,使ED:AD=2FC:AC,求证:△BEF是等腰直角三角形.考点:全等三角形的判定与性质,等腰直角三角形,正方形的性质
专题:
分析:过F作GH∥CD,交AD于G,交BC于H,求出EG=FH,BH=FG,证出RT△BHF≌RT△FGE,推出BF=EF,∠EFG=∠FBH,求出∠EFB=90°,即可得出答案.
解答: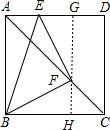 证明:过F作GH∥CD,交AD于G,交BC于H,
证明:过F作GH∥CD,交AD于G,交BC于H,
则有GD:AD=FC:AC①,
而已知ED:AD=2FC:AC②,
由①②得ED=2GD,
即EG=GD(G为ED中点),
即EG=GD=HC=FH,
∵BH=BC-HC且GF=GH-FH,GH=CD=BC,
∴BH=GF,
在RT△BHF和RT△FGE中
∴RT△BHF≌RT△FGE(SAS),
∴BF=EF,∠EFG=∠FBH,
∵∠EGF=90°,
∴∠GEF+∠EFG=90°,
∴∠EFG+∠BFH=90°,
∴∠EFB=180°90°=90°,
∴△BEF是等腰直角三角形.
 证明:过F作GH∥CD,交AD于G,交BC于H,
证明:过F作GH∥CD,交AD于G,交BC于H,则有GD:AD=FC:AC①,
而已知ED:AD=2FC:AC②,
由①②得ED=2GD,
即EG=GD(G为ED中点),
即EG=GD=HC=FH,
∵BH=BC-HC且GF=GH-FH,GH=CD=BC,
∴BH=GF,
在RT△BHF和RT△FGE中
|
∴RT△BHF≌RT△FGE(SAS),
∴BF=EF,∠EFG=∠FBH,
∵∠EGF=90°,
∴∠GEF+∠EFG=90°,
∴∠EFG+∠BFH=90°,
∴∠EFB=180°90°=90°,
∴△BEF是等腰直角三角形.
点评:此题考查了全等三角形的判定与性质,正方形的性质的应用,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
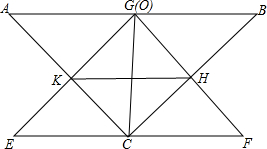 如图所示,在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,现将一个三角板EGF的直角顶点G放在点O处,把△EFG绕点O旋转,EG交直线AC于点K,FG交直线BC于点H.
如图所示,在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,现将一个三角板EGF的直角顶点G放在点O处,把△EFG绕点O旋转,EG交直线AC于点K,FG交直线BC于点H. 有理数a、b在数轴上的位置如图所示:化简|a-b|-(-a)-|b|=
有理数a、b在数轴上的位置如图所示:化简|a-b|-(-a)-|b|= 如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④∠B=∠E,其中能使△ABC≌△AED的条件有
如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④∠B=∠E,其中能使△ABC≌△AED的条件有