题目内容
已知△ABC的三个顶点在圆O上(∠BAC是钝角),高AD、BE相交于点H,直线AD交圆O于点F,求证:DH=DF.
考点:全等三角形的判定与性质,圆周角定理
专题:证明题
分析:连接BF,利用同角的余角相等得到∠H=∠C,再利用同弧所对的圆周角相等及对顶角相等得到两对角相等,进而确定出∠H=∠F,再由一对直角相等,BD为公共边,利用AAS得到三角形HDB与三角形FDB全等,利用全等三角形对应边相等即可得证.
解答:证明: 连接BF,
连接BF,
∵∠HBC+∠H=90°,∠C+∠HBC=90°,
∴∠H=∠C,
∵∠C=∠F,
∴∠H=∠F,
在△HDB和△FBD中,
,
∴△HDB≌△FDB(AAS),
∴DH=DF.
 连接BF,
连接BF,∵∠HBC+∠H=90°,∠C+∠HBC=90°,
∴∠H=∠C,
∵∠C=∠F,
∴∠H=∠F,
在△HDB和△FBD中,
|
∴△HDB≌△FDB(AAS),
∴DH=DF.
点评:此题考查了全等三角形的判定与性质,以及圆周角定理,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 如图,某人在D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度为i=
如图,某人在D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度为i=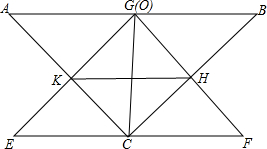 如图所示,在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,现将一个三角板EGF的直角顶点G放在点O处,把△EFG绕点O旋转,EG交直线AC于点K,FG交直线BC于点H.
如图所示,在△ABC中,AC=BC,∠ACB=90°,O为AB的中点,现将一个三角板EGF的直角顶点G放在点O处,把△EFG绕点O旋转,EG交直线AC于点K,FG交直线BC于点H.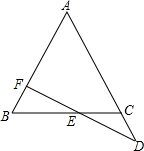 如图,在△ABC中,AB=AC,直线FD交AB于点F,交BC于点E,交AC的延长线于点D,且CD=BF,求证:FE=ED.
如图,在△ABC中,AB=AC,直线FD交AB于点F,交BC于点E,交AC的延长线于点D,且CD=BF,求证:FE=ED.