题目内容
若点P(x,y)在函数y=
+
的图象上,那么点P在平面直角坐标系中第 象限.
| 1 |
| x2 |
| -x |
考点:函数关系式
专题:
分析:因为分式有意义的条件是分母不等于0;二次根式有意义的条件是被开方数大于或等于0.从而可以得到x<0,由x2>0,
≥0可以得>0,∴y=
+
>0,即求出点P所在的象限.
| -x |
| 1 |
| x2 |
| -x |
解答:解:∵
,∴x<0,
又∵x<0,∴
+
>0,即y>0,
∴P应在平面直角坐标系中的第二象限.
故答案为:二.
|
又∵x<0,∴
| 1 |
| x2 |
| -x |
∴P应在平面直角坐标系中的第二象限.
故答案为:二.
点评:本题考查了分式和二次根式有意义的条件,难点是判断出所求的点的横、纵坐标的符号.

练习册系列答案
相关题目
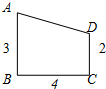 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( )
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( )| A、10或8 | ||||
B、4
| ||||
C、10或4
| ||||
D、10或2
|
 如图一个正方体盒子棱长为50cm,在A处有一只蚂蚁吃到B处食物,则它最少要爬路程为多少?
如图一个正方体盒子棱长为50cm,在A处有一只蚂蚁吃到B处食物,则它最少要爬路程为多少?