题目内容
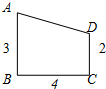在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角梯形，其中三边长分别为2、4、3，则原直角三角形纸片的斜边长是（ ）| A、10或8 | ||||
B、4
| ||||
C、10或4
| ||||
D、10或2
|
考点：图形的剪拼
专题：
分析：先根据题意画出图形，再根据勾股定理求出斜边上的中线，最后即可求出斜边的长．
解答：解：①如图：
因为ED=
=2
，
点D是斜边EF的中点，
所以EF=2ED=4
，
②如图：
因为AE=
=5，
点E是斜边EF的中点，
所以EF=2AE=10，
原直角三角形纸片的斜边长是10或4
，
故选C．
因为ED=
| 22+42 |
| 5 |
点D是斜边EF的中点，
所以EF=2ED=4
| 5 |
②如图：
因为AE=
| 32+42 |
点E是斜边EF的中点，
所以EF=2AE=10，
原直角三角形纸片的斜边长是10或4
| 5 |
故选C．
点评：此题考查了图形的剪拼，解题的关键是能够根据题意画出图形，在解题时要注意分两种情况画图，不要漏解．
练习册系列答案
相关题目
不等式组
的解集为（ ）
|
| A、2＜x≤4 | B、x≤4 |
| C、x＞2 | D、x＜2 |
正方形有而矩形不一定有的性质是（ ）
| A、四个角都是直角 |
| B、对角线相等 |
| C、对角线互相平分 |
| D、对角线互相垂直 |
如图，将四边形纸片ABCD沿EF折叠，点A落在A1处，若∠1+∠2=100°，则∠A的度数是（ ）| A、80° | B、60° |
| C、50° | D、40° |
一个不透明的袋中有形状和大小完全一样的8个小球，其中4个红色，2个黄色，2个白色，从袋中任意地同时摸出3个球，能摸到红球、黄球、蓝球的这件事件（ ）
| A、可能发生 | B、不可能发生 |
| C、很可能发生 | D、必然发生 |
下列函数中，既是一次函数，又是正比例函数的是（ ）
| A、y=15x2 | ||
| B、y=x（x-5）-x2 | ||
C、y=
| ||
| D、y=5x-1 |