题目内容
6.如图,正方形ABCD边BC上一点E,BC=nEC,以AE为边作等腰直角三角形AEF,∠AEF=90°,点G为AF的中点,连接DG.(1)当n=1时,如图①,则$\frac{EC}{GD}$=$\sqrt{2}$;
(2)当n>1时,如图②,则$\frac{EC}{GD}$=$\sqrt{2}$,并说明理由.
(3)连接CF,如图③,当n=$\sqrt{2}$+1时,CF=2CE.
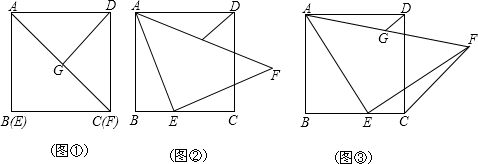
分析 (1)设正方形ABCD的边长为1,根据正方形的性质得出AB=BC=CD=AD=EC=1,∠ABC=∠ADC=90°,根据勾股定理求出AC,求出DG即可;
(2)过点F作FM⊥BC,交BC的延长线于点GM,倍长DG至K,连FK交CD于点H、连接EK,证△ABE≌△EGF,推出FG=BE,AB=EG=BC,证△ADG≌△FKG,推出∠ADG=∠FKG,AD=KF=EM=AB=BC,求出DK=$\sqrt{2}$KH=$\sqrt{2}$EC即可;
(3)BC=($\sqrt{2}$+1)CE,设CE=1,则BC=AB=EM=$\sqrt{2}$+1,求出BE=CM=FM=$\sqrt{2}$,由勾股定理求出CF即可.
解答 解:(1)设正方形ABCD的边长为1,
则AB=BC=CD=AD=EC=1,∠ABC=∠ADC=90°,
由勾股定理得:AC=$\sqrt{2}$,
∵G为AC中点,∠ADC=90°,
∴DG=$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$,
∴$\frac{EC}{GD}$=$\frac{1}{\frac{\sqrt{2}}{2}}$=$\sqrt{2}$,
故答案为:$\sqrt{2}$;
(2)是$\sqrt{2}$,
理由如下:过点F作FM⊥BC,交BC的延长线于点GM,倍长DG至K,连FK交CD于点H、连接EK,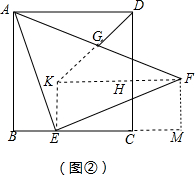
∵∠B=∠AEF=90°,
∴∠BAE+∠AEB=90°,∠AEB+∠FEM=90°,
∴∠BAE=∠FEM,
∵∠B=∠M=90°,
∴在△ABE和△EMF中
$\left\{\begin{array}{l}{∠B=∠M}\\{∠BAE=∠FEM}\\{AE=EF}\end{array}\right.$
∴△ABE≌△EGF,
∴FG=BE,AB=EG=BC,
∴CG=BE=FG,
∵G为AF中点,
∴AG=FG,
∵在△AGD和△FGK中
$\left\{\begin{array}{l}{DG=GK}\\{∠AGD=∠FGK}\\{AG=GF}\end{array}\right.$
∴△ADG≌△FKG,
∴∠ADG=∠FKG,AD=KF=EM=AB=BC,
∴KF∥EG,KF=EG,
∴四边形KFGE为矩形,
∴CH=FG=CG,
∴EC=KH=DH,
∴△DHK为等腰直角三角形,
∴DK=$\sqrt{2}$KH=$\sqrt{2}$EC,
∴$\frac{EC}{GD}=\sqrt{2}$,
故答案为:$\sqrt{2}$;
(3)n=$\sqrt{2}$+1,
理由是:BC=($\sqrt{2}$+1)CE,
设CE=1,则BC=AB=EM=$\sqrt{2}$+1,
所以BE=CM=FM=$\sqrt{2}$,
在Rt△FMC中,由勾股定理得:FC=2,
即CF=2CE,
故答案为:$\sqrt{2}$+1.
点评 本题考查了正方形的性质,直角三角形的性质,全等三角形的性质和判定,平行四边形的性质和判定,勾股定理等知识点的应用,能综合运用性质进行推理和计算是解此题的关键,难度偏大.

| A. | 8个 | B. | 7个 | C. | 5个 | D. | 6个 |
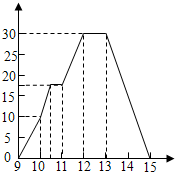 观察如图的折线图,用一段话叙述与图相关的内容,要求用上图中所涉及的数值至少6个,并设法用上速度一词,字数200~400字.
观察如图的折线图,用一段话叙述与图相关的内容,要求用上图中所涉及的数值至少6个,并设法用上速度一词,字数200~400字.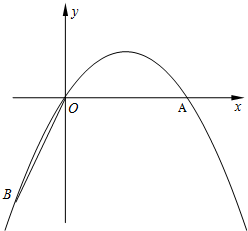 如图,在直角坐标系中,点A的坐标为($2\sqrt{3}$,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
如图,在直角坐标系中,点A的坐标为($2\sqrt{3}$,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.