题目内容
18.某商品现在的售价为每件60元,每个月可卖出100件,市场调查反映:如调整价格,每降价1元,每个月可卖出1件,每涨价1元,每个月要少卖出2件,已知商品的进价为每件40元,售价每件不低于50元,且不高于80元,设每件商品的售价为x元(x为正整数),每个月的销售利润为y元(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?
(3)当每件商品的售价高于60元,定价为多少元使得每个月的利润恰为2250元?
分析 (1)设售价为x元,利润为y,降价时,则每件的利润是(x-40)元,所售件数是[100+(60-x)]件,总利润为y1;根据利润=每件的利润×所售的件数,即可列出函数解析式;涨价时,则每件的利润是(x-40)元,所售件数是[100-2(x-60)]件,总利润为y2;
(2)根据函数的性质即可求得如何定价才能使利润最大;
(3)令y1=2250和y2=2250解一元二次方程即可.
解答 解:(1)设售价为x元,利润为y,
则y1=(x-40)[100+(60-x)]
=-x2+200x-6400.
y2=(x-40)[100-2(x-60)]
=-2x2+240x-6400
∵售价每件不低于50元,且不高于80元,
∴50≤x≤80,
(2)y1=-x2+200x-6400=-(x-100)2+3600.
∵50≤x≤80,-1<0,
∴当x=80时,y的最大值为3200.
y2=-2x2+240x-6400=-2(x-60)2+800.
∴当x=60时,y的最大值为800.
综上所述,当x=80时,y的最大值为3200.
(3)令y1=2250,则2250=-(x-100)2+3600,
整理得:(x-100)2=1350,
x=100±15$\sqrt{6}$
∴当x=100-15$\sqrt{6}$≈63.25,
令y2=2250,则2250=-2x2+240x-6400,
整理得:x2-120x+4325=0
△=14400-17300<0,
故此方程无解.
∴当每件商品的售价高于60元,定价为63.25元使得每个月的利润恰为2250元.
点评 本题考查了二次函数的应用;得到每月卖出商品的件数是解决本题的难点;得到月获得总利润的关系式是解决本题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
10.如果|a|=3,|b|=7,那么|a+b|=( )
| A. | 10 | B. | 4 | C. | 10或4 | D. | -10或-4 |
7.在四边形ABCD中,AB=BC=CD=DA,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
| A. | AC⊥BD | B. | AB∥CD | C. | ∠A=90° | D. | ∠A=∠C |
 如图,△ABC中,∠ABC=60°,点E在边BC上,且EA=EB.
如图,△ABC中,∠ABC=60°,点E在边BC上,且EA=EB.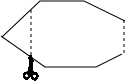 如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为14.
如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为14.