��Ŀ����
15��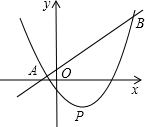 ��ͼ��ֱ��y=kx+2k-1��������y=kx2-2kx-4��k��0���ཻ��A��B���㣬�����ߵĶ���ΪP��
��ͼ��ֱ��y=kx+2k-1��������y=kx2-2kx-4��k��0���ཻ��A��B���㣬�����ߵĶ���ΪP����1�������ߵĶԳ���Ϊֱ��x=1����������Ϊ��1��-k-4�����ú�k�Ĵ���ʽ��ʾ����
��2������kȡ��ֵ���������ܾ������㣬�����Ķ����м�������д�����ж�������꣬�Ƿ��������һ������C��ʹֱ��PC��ֱ��y=kx+2k-1ƽ�У���������ڣ���˵�����ɣ�������ڣ���ֱ��y=kx+2k-1�������ߵĶԳ���Ľ���Q���P����x��Գ�ʱ��ֱ��PC�Ľ���ʽ��
���� ��1�����ݶԳ��ṫʽ������öԳ���Ϊx=1��Ȼ���x=1������뼴����ö������ꣻ
��2���ѽ���ʽ����Ϊy=kx2-2kx-4=k��x-2��x-4����������������ܾ����Ķ��㣻���ݶ���P���Q�����꣬����ֱ�߽���ʽ���k��ֵ���ó�P��1��-$\frac{13}{2}$��������ƽ�е��������PC�Ľ���ʽ��Ȼ����ݴ���ϵ����������ã�
��� �⣺��1����������y=kx2-2kx-4��k��0����
��Գ���Ϊֱ��x=-$\frac{-2k}{2•k}$=1��
��x=1ʱ��y=k-2k-4=-k-4��
�ඥ��PΪ��1��-k-4����
�ʴ�Ϊֱ��x=1����1��-k-4����
��2����y=kx2-2kx-4=k��x-2��x-4��֪������kȡ��ֵ���������ܾ������㣨0��-4���ͣ�2��-4�������㣬
�߽���Q���P����x��Գƣ�
��Q��1��k+4����
��ֱ��y=kx+2k-1�������ߵĶԳ���Ľ���ΪQ��
��k+4=k+2k-1�����k=$\frac{5}{2}$��
��P��1��-$\frac{13}{2}$����
����PC��ֱ��y=kx+2k-1ƽ�У�
����ֱ��PC�Ľ���ʽΪy=$\frac{5}{2}$x+b��
����P��1��-$\frac{13}{2}$����-$\frac{13}{2}$=$\frac{5}{2}$+b��
���b=-9��
��ֱ��PC�Ľ���ʽΪy=$\frac{5}{2}$x-9��
�ʴ��ڶ���C��ʹֱ��PC��ֱ��y=kx+2k-1ƽ�У�ֱ��PC�Ľ���ʽΪy=$\frac{5}{2}$x-9��
���� ������Ҫ�����˶��κ��������ʺ�һ�κ��������ʣ�����Ĺؼ�������ƽ�е����ʺ���ԳƵ����ʵó�P�����꣮

| A�� | ����������ȵ��������ǵ��������� | |
| B�� | ͬλ����� | |
| C�� | ���|a|=|b|����ôa=b | |
| D�� | �����ȵ�����������ȫ�� |
| A�� |  | B�� |  | ||
| C�� |  | D�� |  |
 ��ͼ��?ABCD�У�BC=BD����C=72�㣬���ADB�Ķ����ǣ�������
��ͼ��?ABCD�У�BC=BD����C=72�㣬���ADB�Ķ����ǣ�������| A�� | 18�� | B�� | 26�� | C�� | 36�� | D�� | 72�� |
| A�� | ������ | B�� | ������� | C�� | �������� | D�� | ˮ������ |

��ô��671��ͼ�������ӵĸ���Ϊ��������
| A�� | 2016 | B�� | 2015 | C�� | 2014 | D�� | 2013 |
 ��ͼ�Ƕ��κ���y=ax2+bx+c��a��0��ͼ���һ���֣��Գ���Ϊx=$\frac{1}{2}$���Ҿ����㣨2��0����������˵������abc��0����a+b=0����a-b+c=0��������0��y1������1��y2�����������ϵ����㣬��y1=y2������˵����ȷ���ǣ�������
��ͼ�Ƕ��κ���y=ax2+bx+c��a��0��ͼ���һ���֣��Գ���Ϊx=$\frac{1}{2}$���Ҿ����㣨2��0����������˵������abc��0����a+b=0����a-b+c=0��������0��y1������1��y2�����������ϵ����㣬��y1=y2������˵����ȷ���ǣ�������| A�� | �٢ڢۢ� | B�� | �ۢ� | C�� | �٢ۢ� | D�� | �٢� |
| A�� | m��y1��y2 | B�� | m��y2��y1 | C�� | y1��y2��m | D�� | y2��y1��m |